投影变换的推导

这里我们说到的投影分为两种：

• 正交投影(Orthographic projection (O))
• 透视投影(Perspective projection (P))

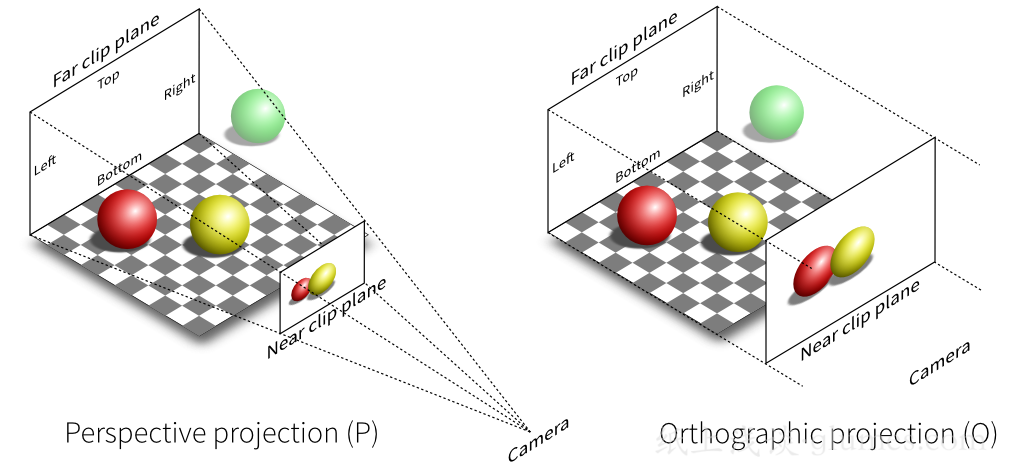
正交投影(Orthographic projecton)

先来说一说最简单的正交投影，我们需要做的是：

• 定义一个$[l, r] * [b, t] * [f, n]$的立方体
• 然后将定义的立方体转换成“标准(canonical)”立方体$[-1, 1]^{3}$

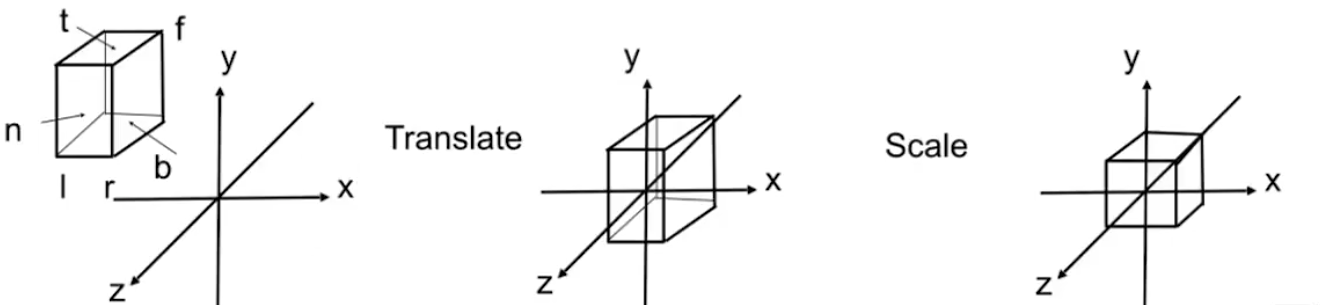
如上图，我们想要把最左边的长方体变成最右边的立方体，需要两步：

• 平移(Translate)
• 缩放(Scale)

平移(Translate)

首先我们要做的操作就是平移，先把长方体的中心点移至原点（origin）。因为我们已经知道l,r,b,t,f,n六个参数，所以我们可以计算出当前长方体的中心点，即：

$$(x, y, z) = (\frac{(r + l)}{2}, \frac{(t + b)}{2}, \frac{(n + f)}{2})$$

那么平移变换矩阵就应该是一个单位矩阵加上平移部分，要想将长方体的中心点移至原点（origin），只需要把所有点都减去长方体的中心点即可。

$$M_{Translate} = \begin{pmatrix} 1 & 0 & 0 & -\frac{(r + l)}{2} \\ 0 & 1 & 0 & -\frac{(t + b)}{2} \\ 0 & 0 & 1 & -\frac{(n + f)}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$$

缩放(Scale)

有了平移变换，接下来要做的就是缩放了，将每个点都等比缩放至$[-1, 1]^{3}$立方体上。那么$[l, r]$和$[-1, 1]$的比例为$\frac{2}{r - l}$，$[b, t]$和$[-1, 1]$的比例为$\frac{2}{t - b}$，$[f, n]$和$[-1, 1]$的比例为$\frac{2}{n - f}$（因为相机照像$-z$方向，所以$n$比$f$大）。

$$M_{Scale} = \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{t - b} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}$$

两种变换相乘

将平移和缩放融合在一起，即两矩阵相乘：

$$\begin{equation}\begin{split} M_{Ortho} &= M_{Scale} * M_{Translate} \\ &= \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{t - b} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} * \begin{pmatrix} 1 & 0 & 0 & -\frac{(r + l)}{2} \\ 0 & 1 & 0 & -\frac{(t + b)}{2} \\ 0 & 0 & 1 & -\frac{(n + f)}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{(r + l)}{r - l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{(t + b)}{t - b} \\ 0 & 0 & \frac{2}{n - f} & -\frac{(n + f)}{n - f} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \\ \end{split}\end{equation}$$

透视投影(Perspective projection)

透视投影相对于正交投影就比较困难了，不过我们可以换一种思路

• 首先，把视锥体(view frustum)挤扁成一个立方体(cuboid)($M_{Persp->Ortho}$)
• 然后，我们通过正交投影，即可把远平面投影至近平面

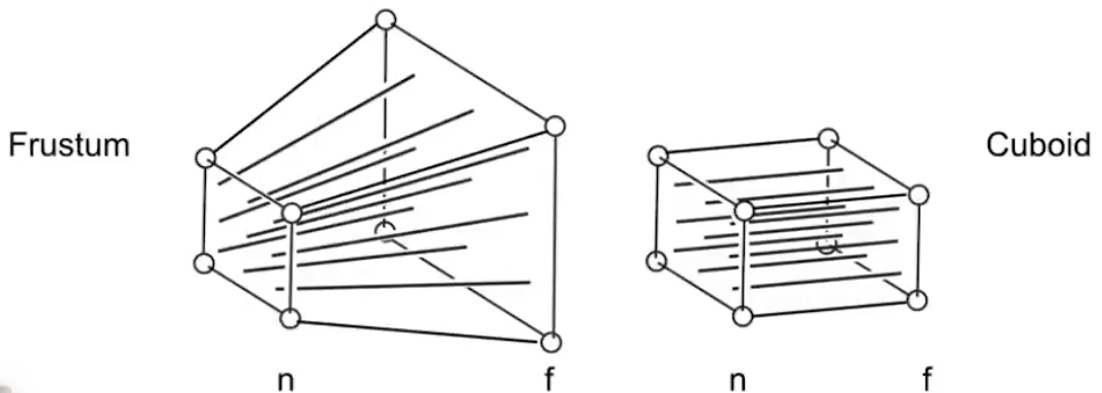
把视锥体(view frustum)挤扁成一个立方体(cuboid)

在挤压的过程中，我们需要规定几件事情：

• 近平面上的任意点都不会改变
• 远平面上的$z$值不变，永远都是$f$
• 远平面上的中心点不变

下面我们来寻找一下近平面和远平面之间的点的关系，从视锥体的右侧观察，如下图：

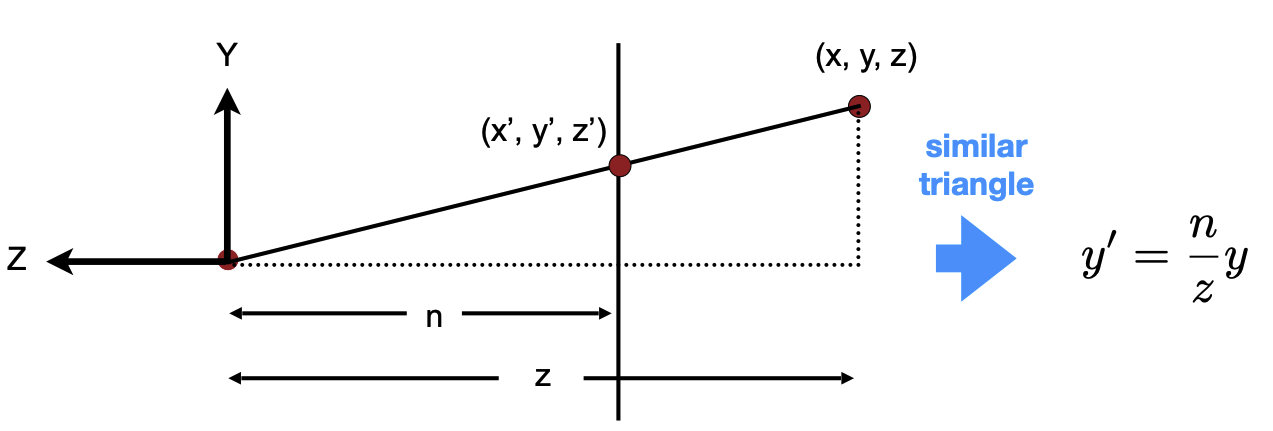
通过相似三角形的性质，可以得出$y^{'} = \frac{n}{z}y$，同理，$x^{'} = \frac{n}{z}x$。

因为$z$暂时未知，那么我们可以得出，点$\begin{pmatrix} x & y & z & 1\end{pmatrix}^{T}$经过变换后，可以得到点$\begin{pmatrix} \frac{nx}{z} & \frac{ny}{z} & unknow & 1\end{pmatrix}^{T}$。

通过齐次坐标，我们可以将点$\begin{pmatrix} \frac{nx}{z} & \frac{ny}{z} & unknow & 1\end{pmatrix}^{T}$转换为点$\begin{pmatrix} nx & ny & unknow & z\end{pmatrix}^{T}$。

所以，

$$M_{Persp->Ortho} · \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix} = \begin{pmatrix} nx \\ ny \\ unknow \\ z\end{pmatrix}$$

根据上述等式，我们已经可以反推出：

$$M_{Persp->Ortho} = \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}$$

那么未知的第三行应该如何推算呢？我们可以思考两个特殊条件：

• 近平面上任意点在做变换后，不会改变
• 远平面上任意点的z值在做变换后，不会改变

近平面上任意点变换后不会改变

取近平面上点$(x, y, n, 1)^{T}$，通过齐次坐标，可以转换为点$(nx, ny, n^{2}, n)^{T}$。则：

$$\begin{equation}\begin{split} M_{Persp->Ortho} · \begin{pmatrix}x \\ y \\ n \\ 1\\ \end{pmatrix} &= \begin{pmatrix}nx \\ ny \\ n^{2} \\ n\\ \end{pmatrix} \\ \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} · \begin{pmatrix}x \\ y \\ n \\ 1\\ \end{pmatrix} &= \begin{pmatrix}nx \\ ny \\ n^{2} \\ n\\ \end{pmatrix}\\ \end{split}\end{equation}$$

我们单独解出变换矩阵的第三行，即：

$$\begin{pmatrix} ? & ? & ? & ? \\ \end{pmatrix} · \begin{pmatrix}x \\ y \\ n \\ 1\\ \end{pmatrix} = n^{2}$$

因为等式结果等于$n^{2}$，与$x$和$y$值并没有关系，所以得出：

$$\begin{pmatrix} 0 & 0 & A & B \\ \end{pmatrix} · \begin{pmatrix}x \\ y \\ n \\ 1\\ \end{pmatrix} = n^{2}$$

可得出（1）式，

$$An + B = n^{2}$$

远平面上任意点的z值变换后不会改变

因为开始时，我们规定远平面中心点在变换后，仍然不改变，所以我们取远平面的中心点$(0, 0, f, 1)^{T}$，通过齐次坐标，我们可以将点转换为$(0, 0, f^{2}, f)^{T}$。

则，

$$\begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ 0 & 0 & A & B \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} · \begin{pmatrix}0 \\ 0 \\ f \\ 1\\ \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ f^{2} \\ f\\ \end{pmatrix}\\$$

因为等式结果等于$f^{2}$，与$x$和$y$值并没有关系，所以得出：

$$\begin{pmatrix} 0 & 0 & A & B \\ \end{pmatrix} · \begin{pmatrix}0 \\ 0 \\ f \\ 1\\ \end{pmatrix} = f^{2}$$

可得出（2）式，

$$Af + B = f^{2}$$

由（1）式和（2）式解得：

$$A = n + f \\ B = -nf$$

所以，得出：

$$M_{Persp->Ortho} = \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}$$

通过正交投影把远平面投影至近平面

正交投影的变换矩阵在上边我们已经求出，且$M_{Persp->Ortho}$也已求出，所以我们可以通过矩阵乘法求得$M_{Persp}$。

即，

$$\begin{equation}\begin{split} M_{Persp} &= M_{Ortho} · M_{Persp->Ortho} \\ &= \begin{pmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{(r + l)}{r - l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{(t + b)}{t - b} \\ 0 & 0 & \frac{2}{n - f} & -\frac{(n + f)}{n - f} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} · \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{2n}{r - l} & 0 & -\frac{r + l}{r - l} & 0 \\ 0 & \frac{2}{t - b} & -\frac{(t + b)}{t - b} & 0 \\ 0 & 0 & \frac{n + f}{n - f} & -\frac{2nf}{n - f} \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \\ \end{split}\end{equation}$$