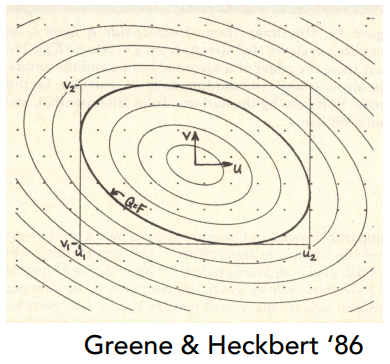
Shading

五月 16, 2021

Games101

Illumination & Shading

Shading: Definition

In Merriam-Webster Dictionary

shad·ing, [ˈʃeɪdɪŋ], noun

The darkening or coloring of an illustration or diagram with parallel lines or a block of color.
In this course

The process of applying a material to an object.

A Simple Shading Model (Blinn-Phong Reflectance Model)

Specular highlights（镜面高光）
Diffuse reflection（漫反射）
Ambient lighting（环境光）

Shading is Local

Compute light reflected toward camera at a specific shading point.

Inputs:

Viewer direction, $ v $
Surface normal, $ n $
Light direction, $ l $ (for each of many lights)
Surface parameters(color, shininess, …)

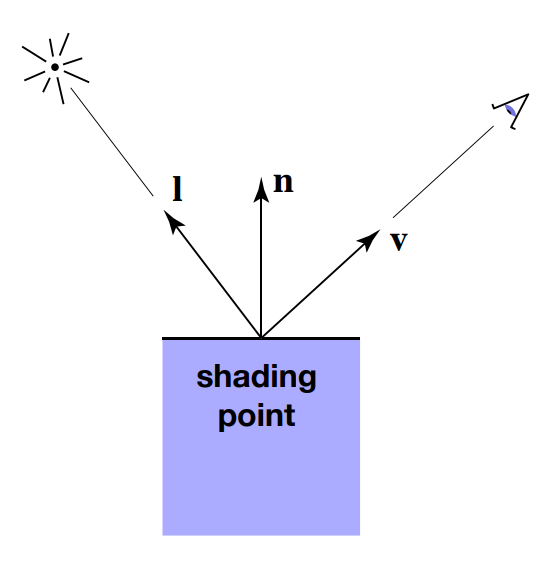
No shadows will be generated! (shading ≠ shadow)

Diffuse Reflection

But how much light (energy) is received?
- Lambert’s cosine law

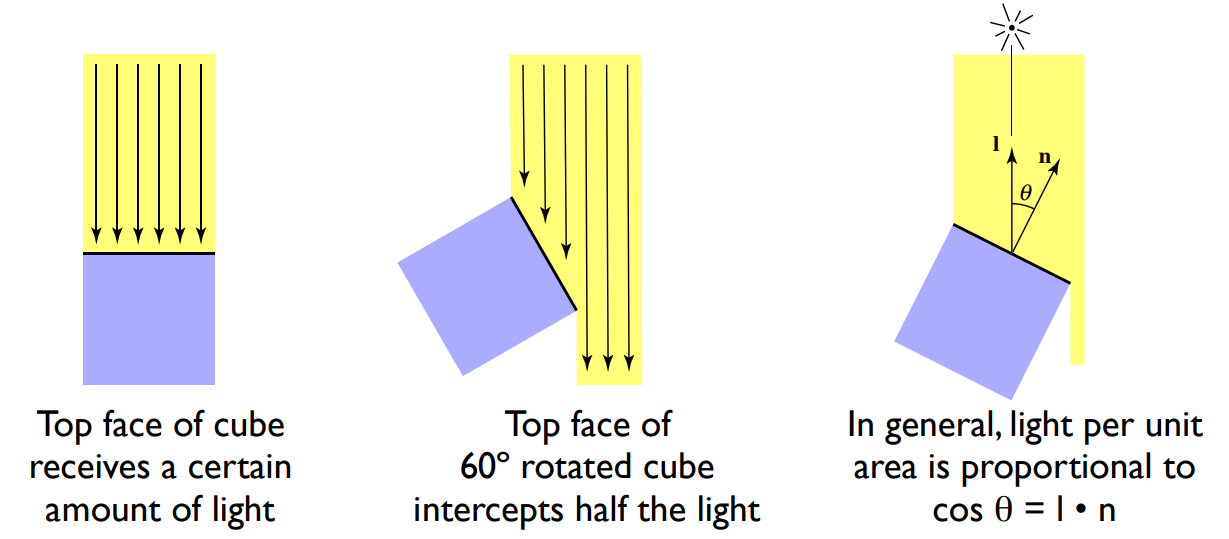
立方体的顶面接收一定量的光
旋转60度的立方体顶面只截取了一半的光
通常，每个单位面积的光与 $\cos(\theta) = l · n$ 成正比

Light Falloff

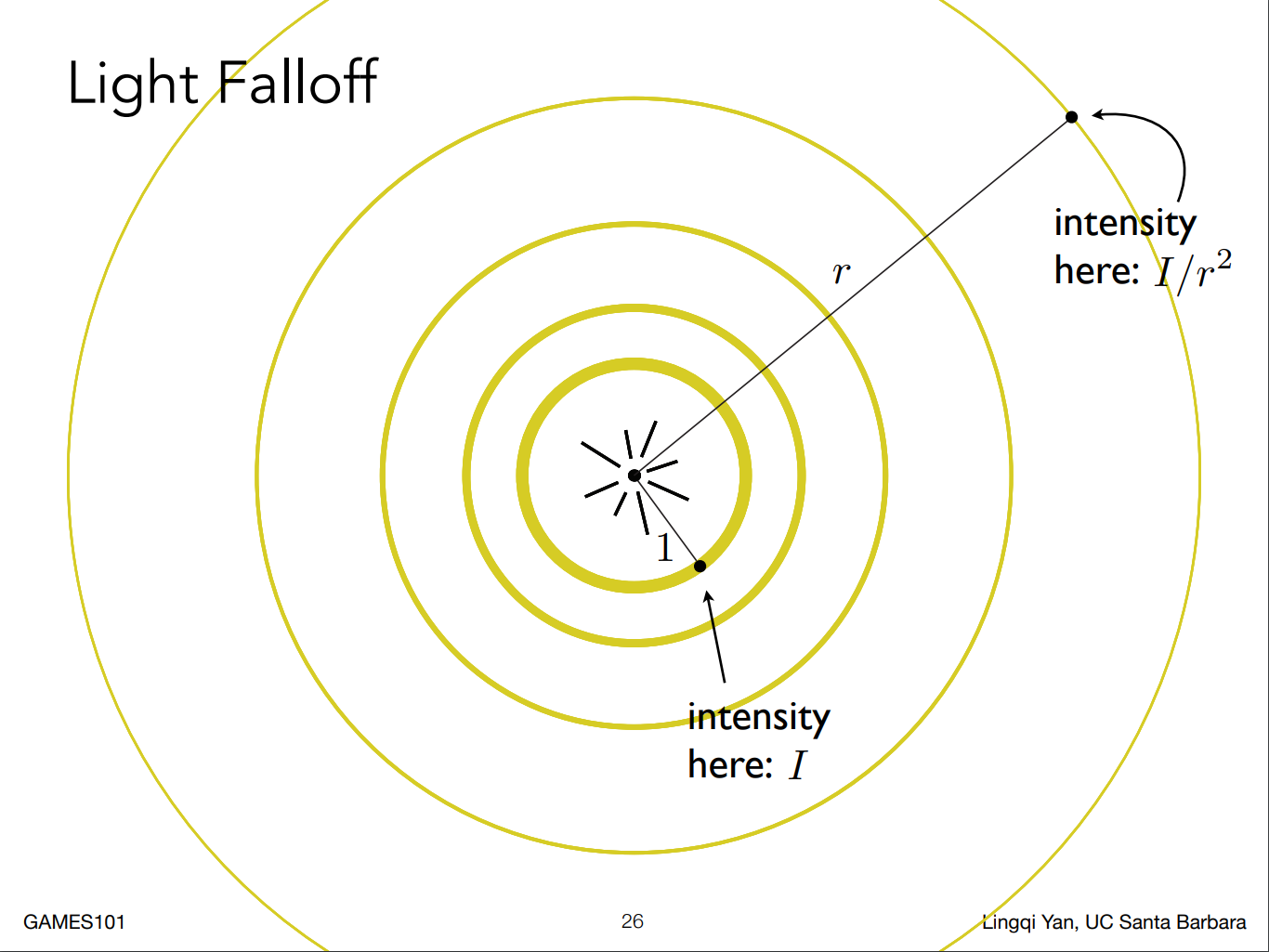
半径为1的球面上，光的强度为I。球的面积公式为 $4\pi R^{2}$ ，所以图中最远处的球面上，光强度为 $I/R^{2}$ 。

Lambertian (Diffuse) Shading

Shading independent of view direction

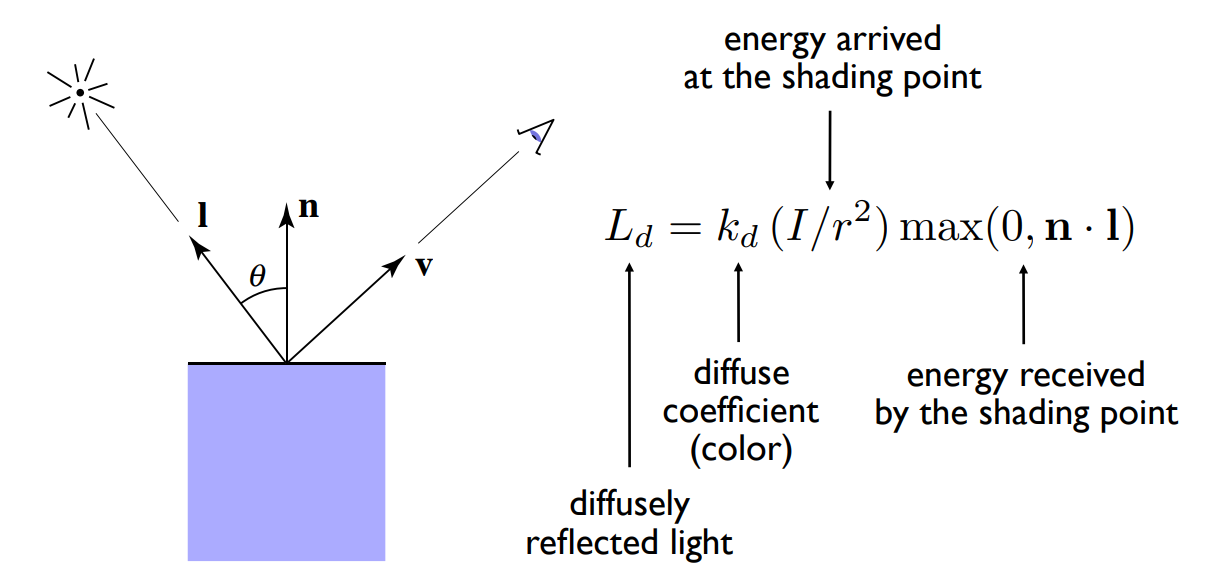
$k_{d}$：漫反射项的系数（vector类型，分别代表RGB，0-1）
- 如果等于1，就代表该点完全不吸收能量，进来多少反射多少
- 如果等于0，就代表该点吸收了所有能量，没有能量反射出去
$I/r^{2}$：到达shading point的能量
$max(0, n · l)$：有多少能量会被接收，因为n和l为单位向量，所以余弦值就是两个向量点乘，如果余弦值为负数，则无物理意义。

漫反射打到一个点上，反射光应该是各个方向均匀分布，所以从哪个角度观察，结果都是一模一样的，所以公式和向量v没有任何关系。

Specular Term (Blinn-Phong)

镜面反射项，Blinn-Phong模型（高光）

镜面反射强度取决于观察方向

接近镜面反射方向

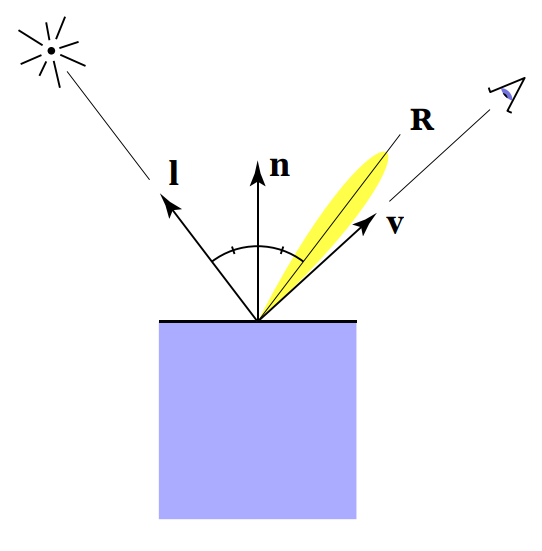
$v$距离镜面反射方向越近，半程向量越接近法向量

用单位向量的点积测量接近程度

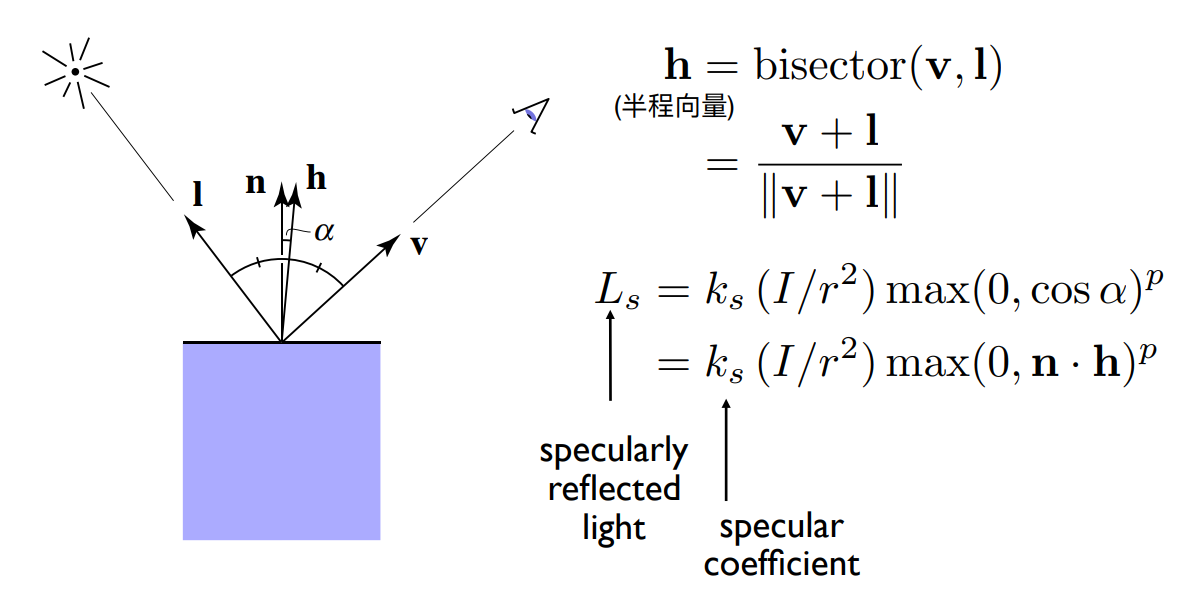
$ k_{s} $：镜面反射系数，通常认为是一个白色
$(I/r^{2})$：到达shading point的能量
$max(0, n·h)^{p}$：使用点乘计算半程向量和法向量的夹角余弦值，从而判断两个向量的接近程度
- n：法向量
- h：半程向量，使用平行四边形法则，向量v加上向量l求出半程向量，除以向量的模得出半程向量的单位向量h
- p：指数，因为余弦值用来判断两个向量的接近程度，容忍度太高，会导致高光面积过大，所以需要加一个指数。正常再Blinn-Phong模型中大概会用到100-200。（如下图)

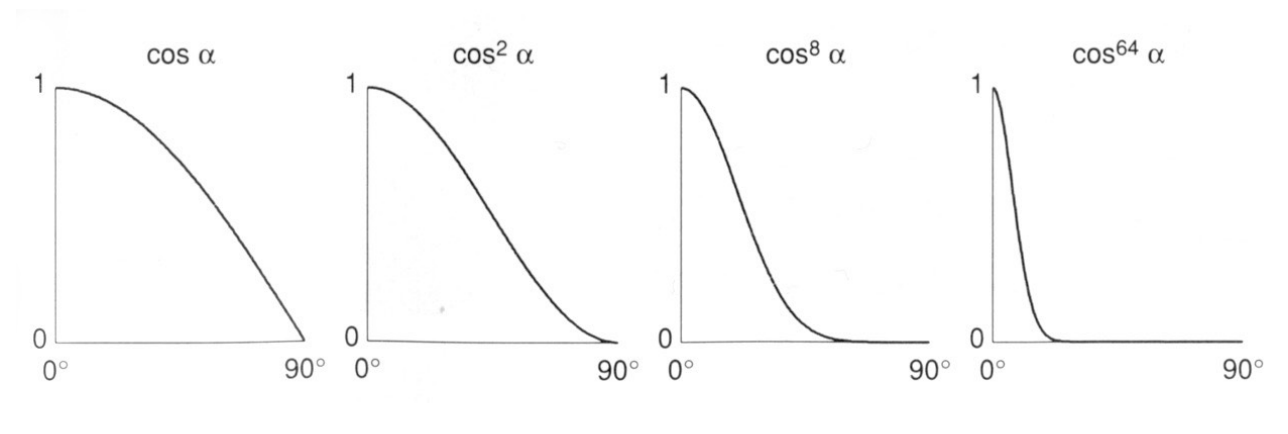
这里因为Blinn-Phong模型是一个经验模型，所以不考虑shading poing有多少能量被吸收。

使用镜面反射向量r和观察向量v做点乘也可以判断这两个向量的远近程度，从而判断高光。此模型被称为Phong模型，Blinn-Phong模型是Phong模型的一个改进，因为半程向量的计算量低于反射向量的计算量。

Ambient Term

环境光

做一个大胆的假设，任何一个点接收到来自环境的光永远都是相同的，强度叫做$ I_{a} $。任何点都有自己的一个颜色，$k_{a}$环境光的系数。把$k_{a}$和$I_{a}$结合在一起，我们就可以近似的得出一个环境光。可以保证没有地方是完全黑色的。

Blinn-Phong Reflection Model

$\begin{equation} \begin{split} L &= L_{a} + L_{d} + L_{s} \\ &= k_{a}I_{a} + k_{d}(I/r^{2})max(0, n·l) + k_{s}(I/r^{2})max(0, n·h)^{p}\\ \end{split} \end{equation}$

Shading Frequencies

Shading Frequency: Face, Vertex or Pixel

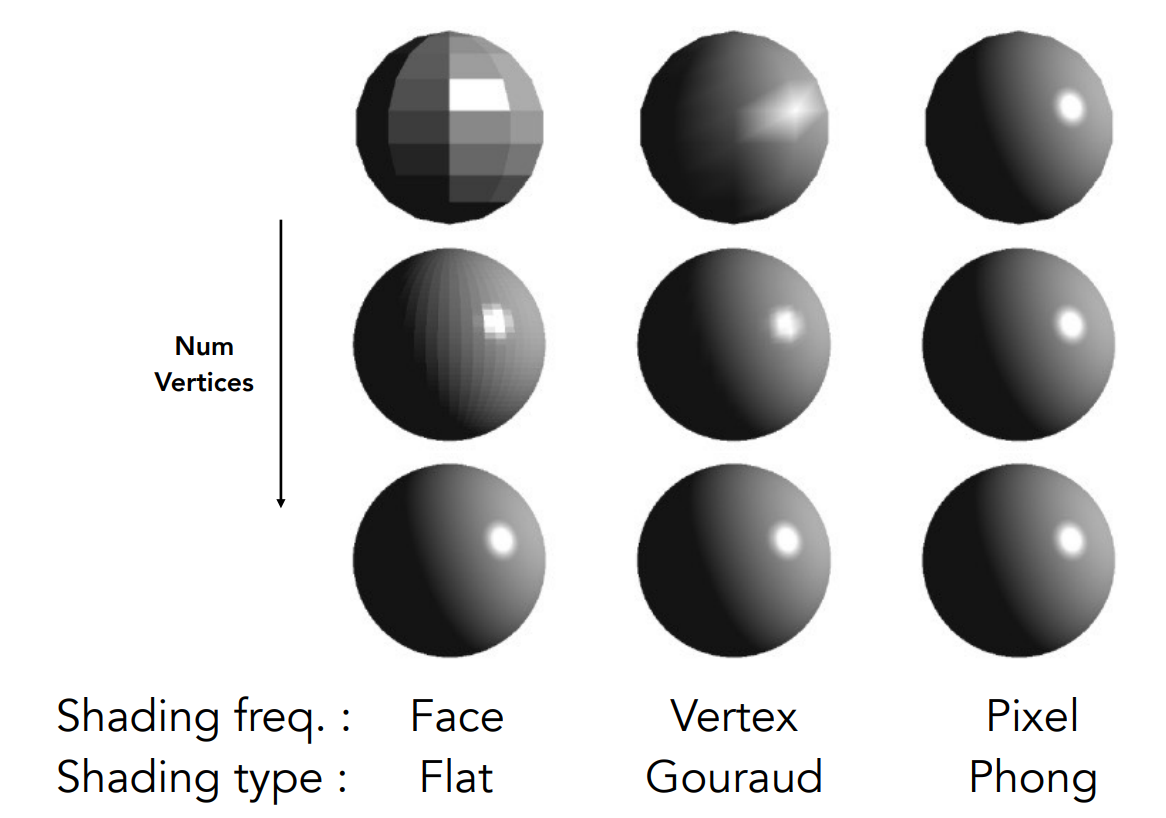
着色频率取决于几何面或者顶点出现的频率，当面出现的频率已经很高的情况下，就不需要使用复杂的逐像素着色。

Defining Per-Vertex Normal Vectors

最好的方法是从基础的集合获取顶点的法线。例如下图（上），当我们知道我们所要渲染的几何是个球体，那么顶点表示的就是球面上的点，可以通过求该顶点所在球面的法线来获取顶点法线。但是现实情况中，并不能够总是渲染一个已知的规则几何。

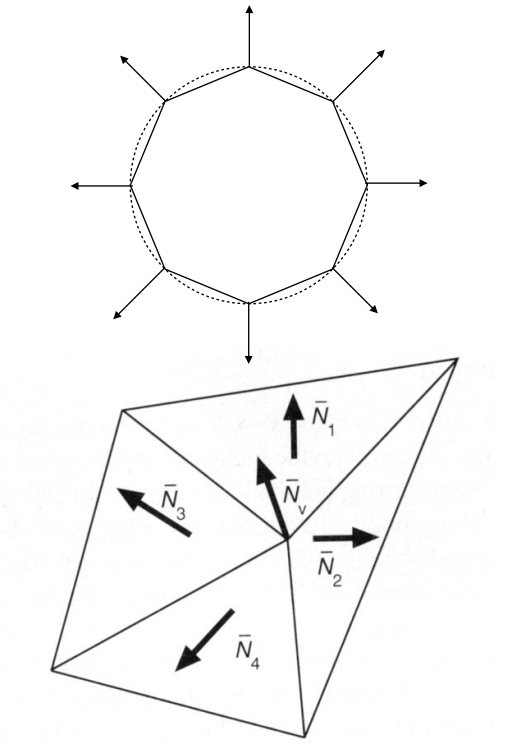
所以我们需要通过三角面的法线来推断顶点法线，其中最简单的方案就是，求顶点所关联的所有面法线之和的平均，然后再做归一化操作，得出该顶点的法线。

$N_{v} = \frac{\sum_i N_{i}}{||\sum_i N_{i}||}$

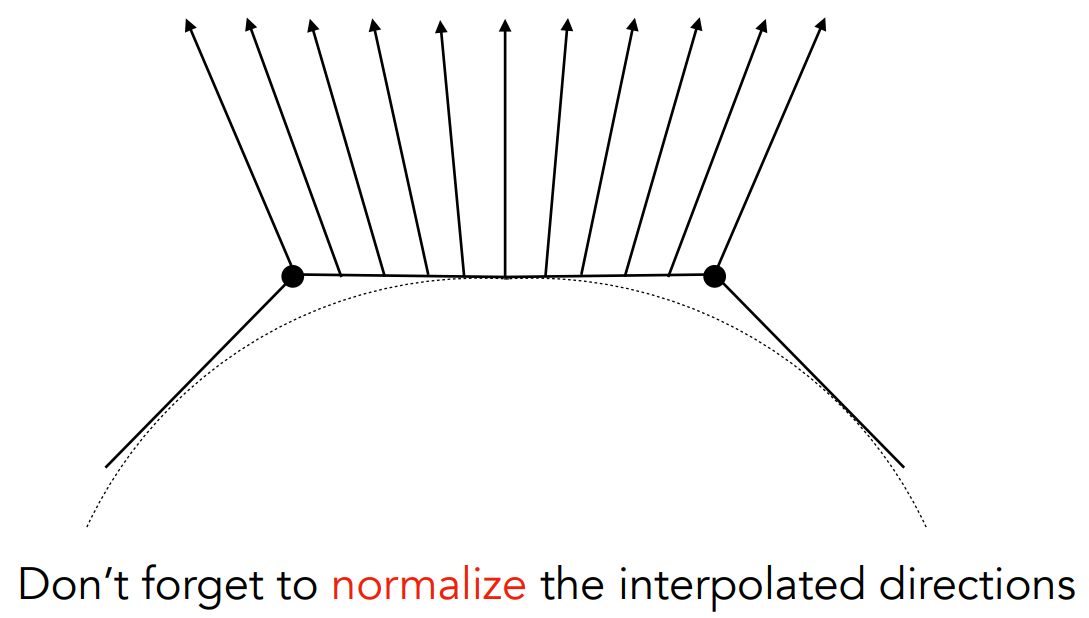
Defining Per-Pixel Normal Vectors

Barycentric interpolation (introducing soon) of vertex normals

顶点法线的重心插值

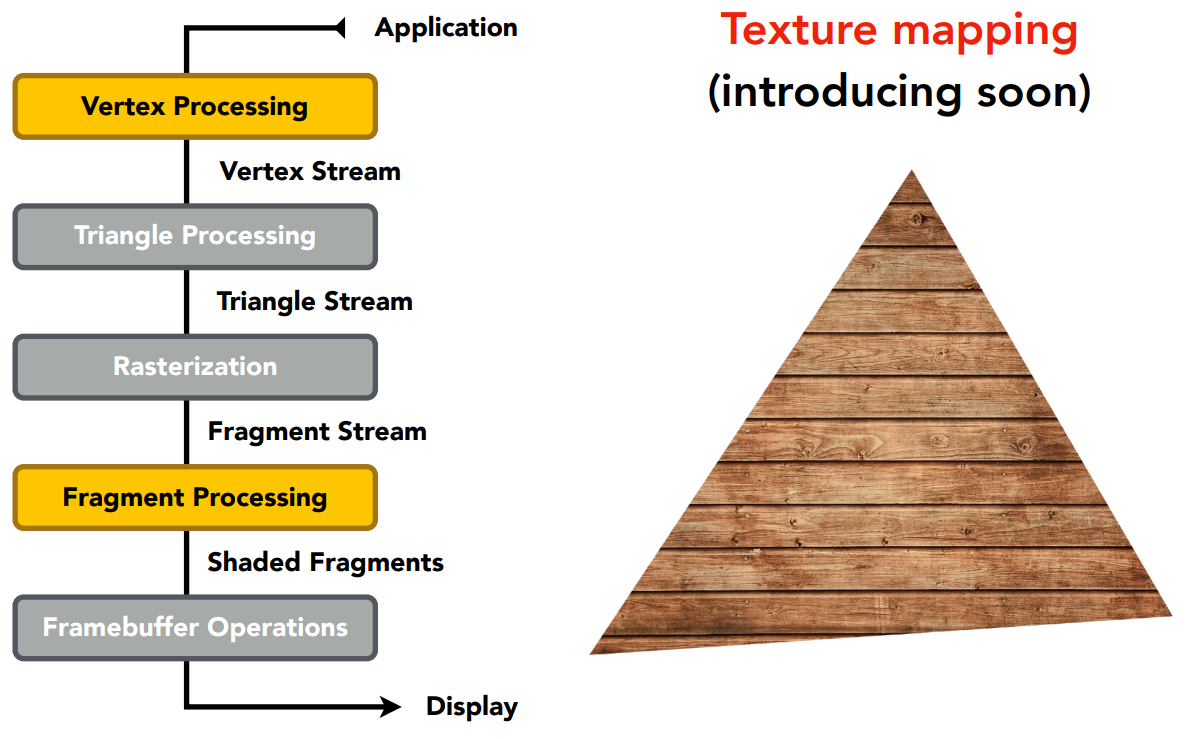
Graphics (Real-time Rendering) Pipeline

图形管线（实时渲染管线）流程

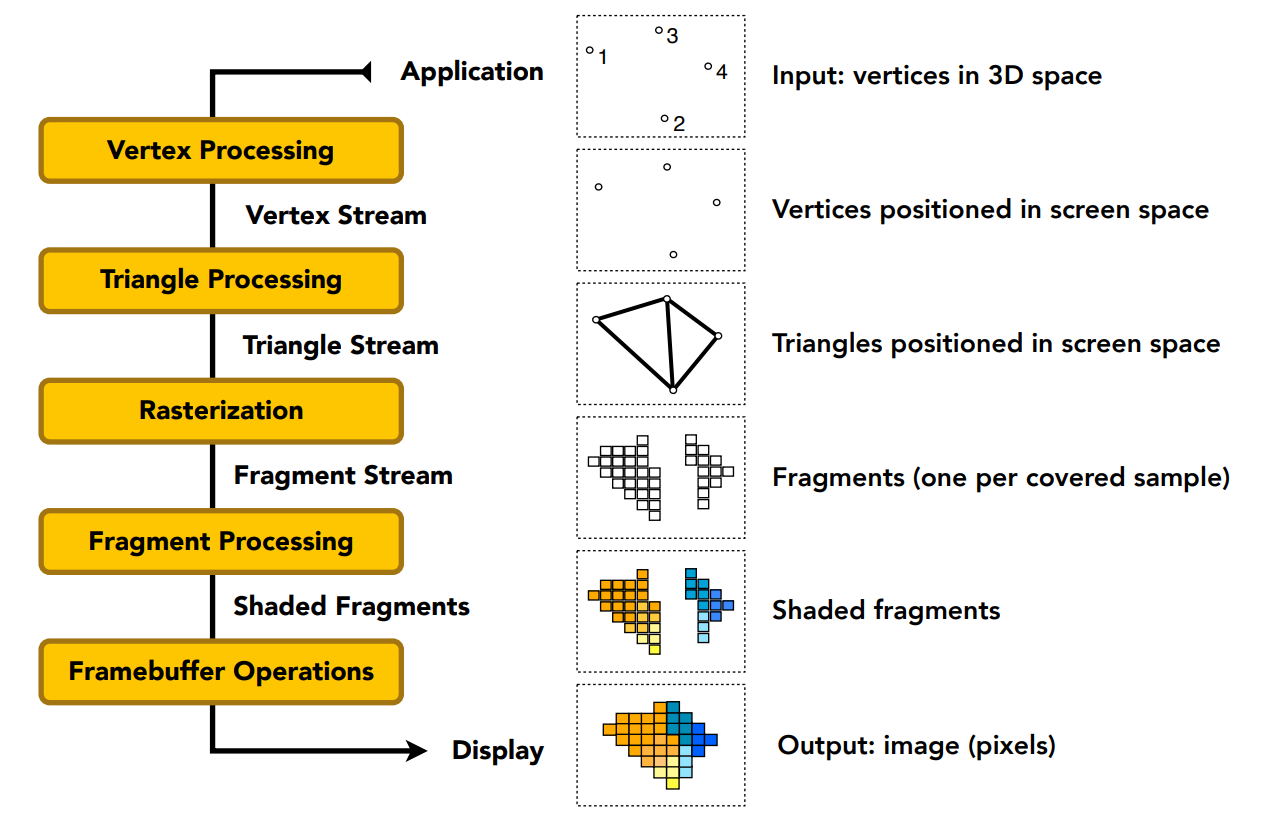
顶点处理，做一些顶点变换

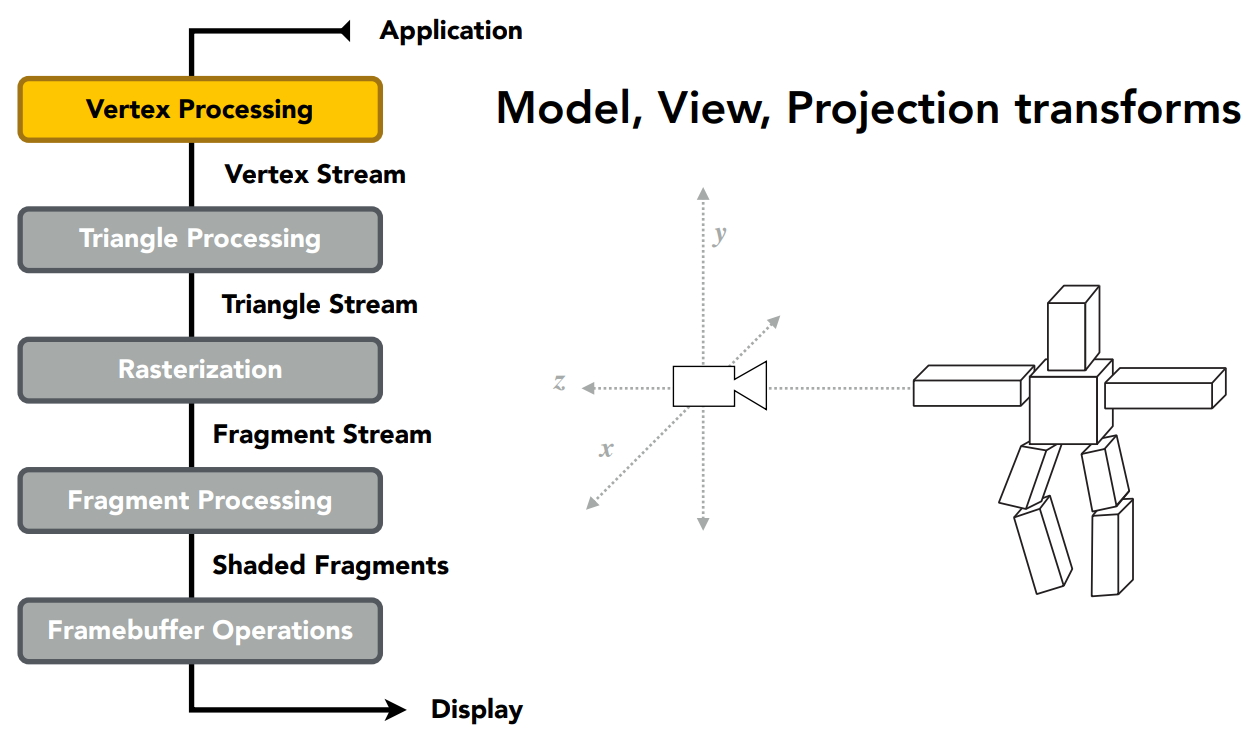
顶点处理和三角形处理后，进行光栅化三角形

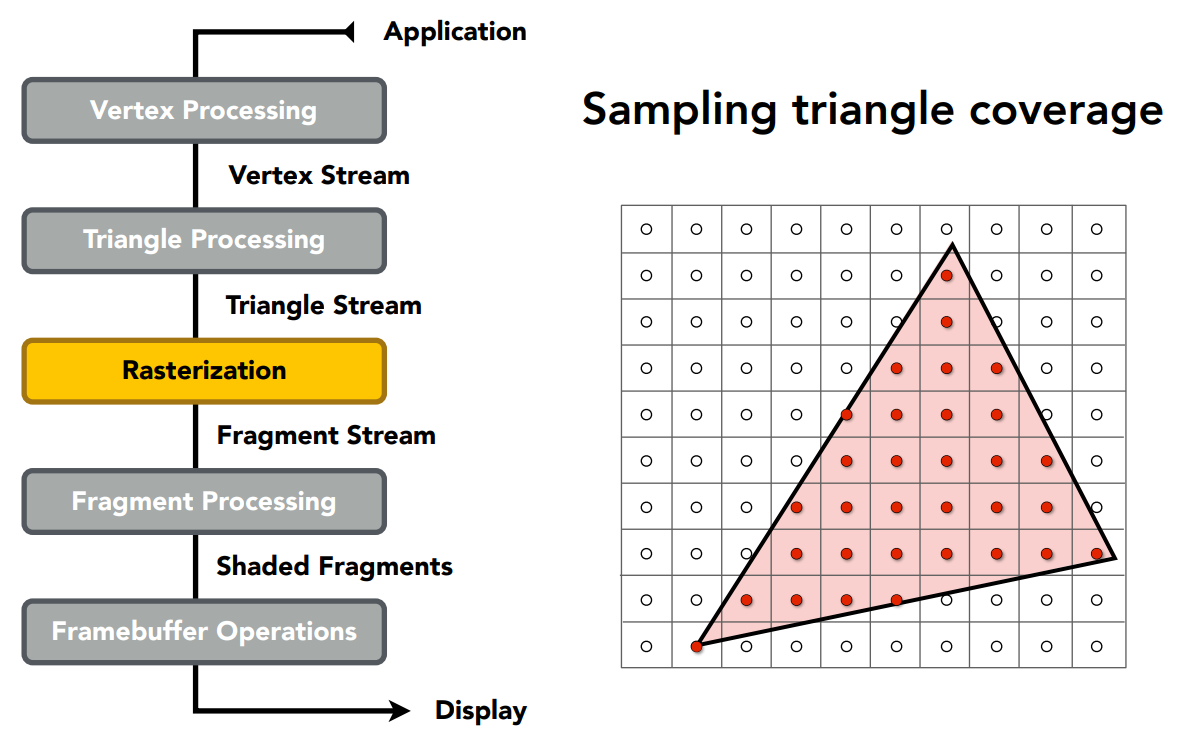
片段（像素）处理，深度测试（有些教材把深度测试归为光栅化阶段）

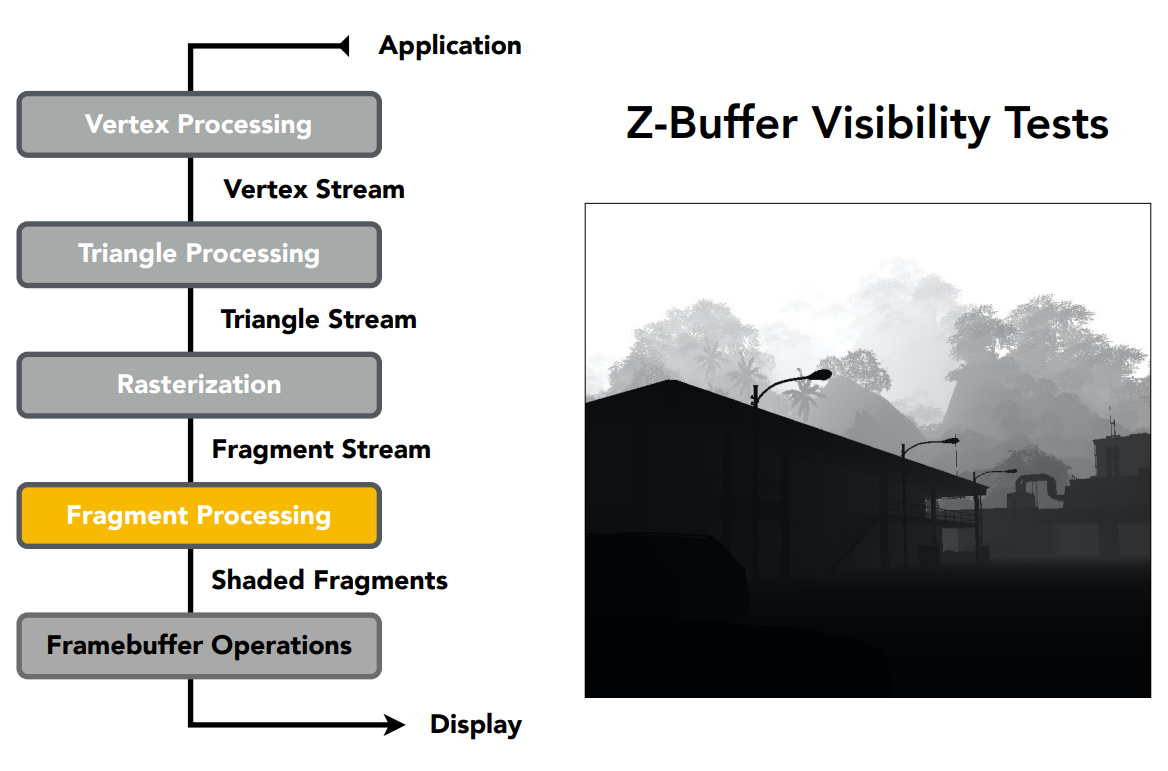
着色阶段有两个

顶点着色，高洛德着色（Gouraud Shading）
片段着色，Phong着色（Phong Shading）。

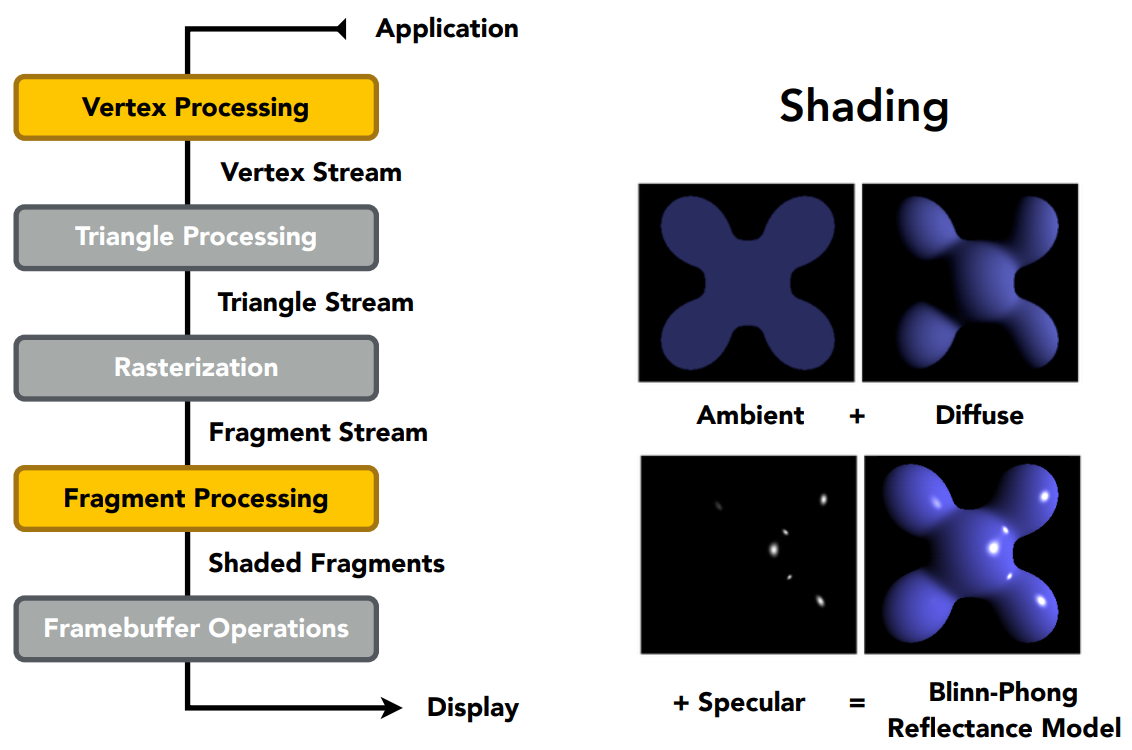
纹理映射

Shader Programs

Vertex shader
Fragment shader

这里拿一个GLSL的片段着色程序来做实例：

着色方法在每个片段上执行一次
在当前片段的屏幕采样点输出表面颜色
该着色器执行纹理查找以获取表面的材质颜色，然后执行漫射照明计算

uniform sampler2D myTexture; // program parameter
uniform vec3 lightDir; // program parameter
varying vec2 uv; // per fragment value (interp. by rasterizer)
varying vec3 norm; // per fragment value (interp. by rasterizer)
void diffuseShader()
{
 vec3 kd;
 kd = texture2d(myTexture, uv); // material color from texture
 kd *= clamp(dot(–lightDir, norm), 0.0, 1.0); // Lambertian shading model
 gl_FragColor = vec4(kd, 1.0); // output fragment color
}

Goal: Highly Complex 3D Scenes in Realtime

100’s of thousands to millions of triangles in a scene
Complex vertex and fragment shader computations
High resolution (2-4 megapixel + supersampling)
30-60 frames per second (even higher for VR)

Texture Mapping

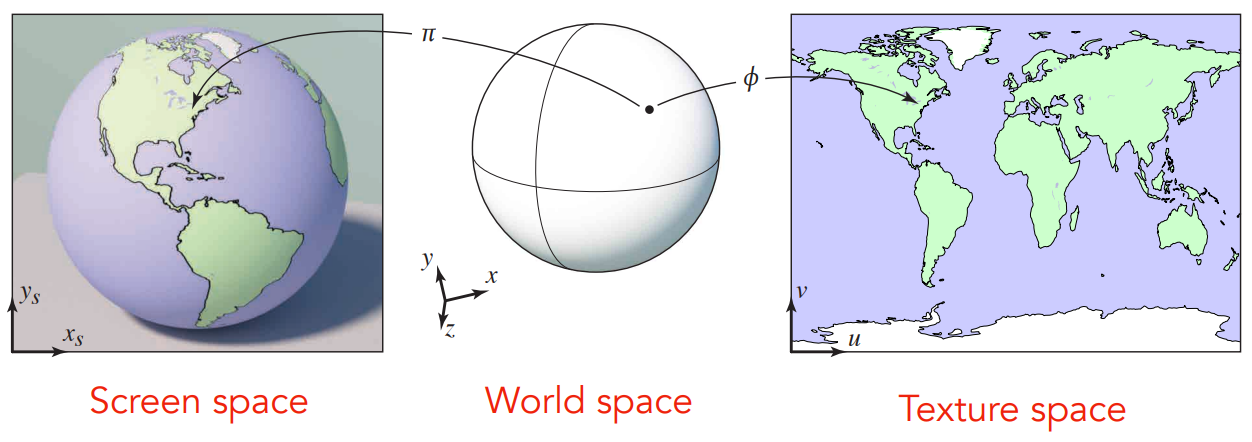
Surfaces are 2D

任何一个三维物体它的表面都是二维的。

任意3D表面上的点都对应2D图片上的一个位置，这个2D图片就称为纹理（Texture）。把这个图片通过拉伸、压缩等方式蒙在3D物体的表面，这个过程就叫做纹理映射（Texture Mapping）。

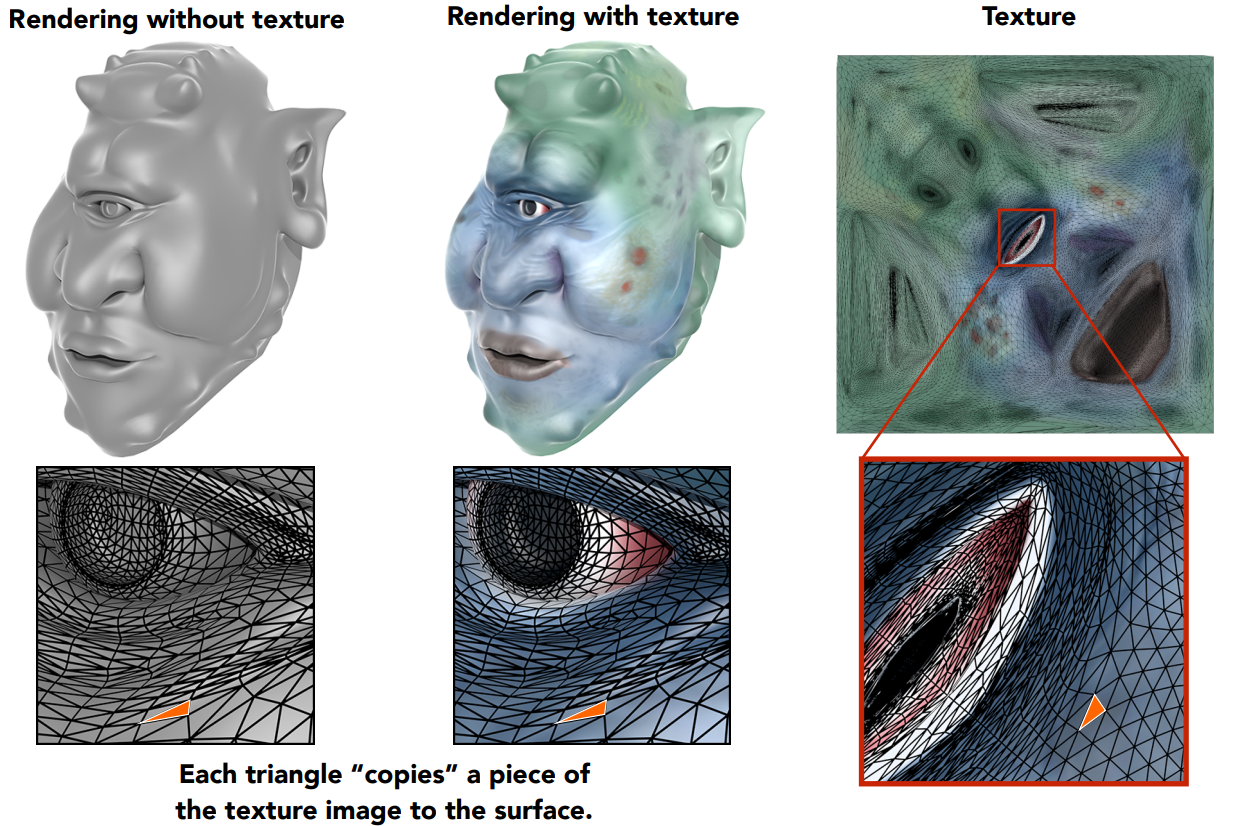
每个三角形将一块纹理图片“拷贝”到表面。

每一个三角形的顶点上都分配有一个纹理坐标（Texture Coordinate，（u,v））

$ u $：代表横向坐标，越红代表值越大
$ v $：代表纵向坐标，越绿代表值越大
坐标值在区间$ [0,1] $上，方便计算任何分辨率大小的纹理的坐标

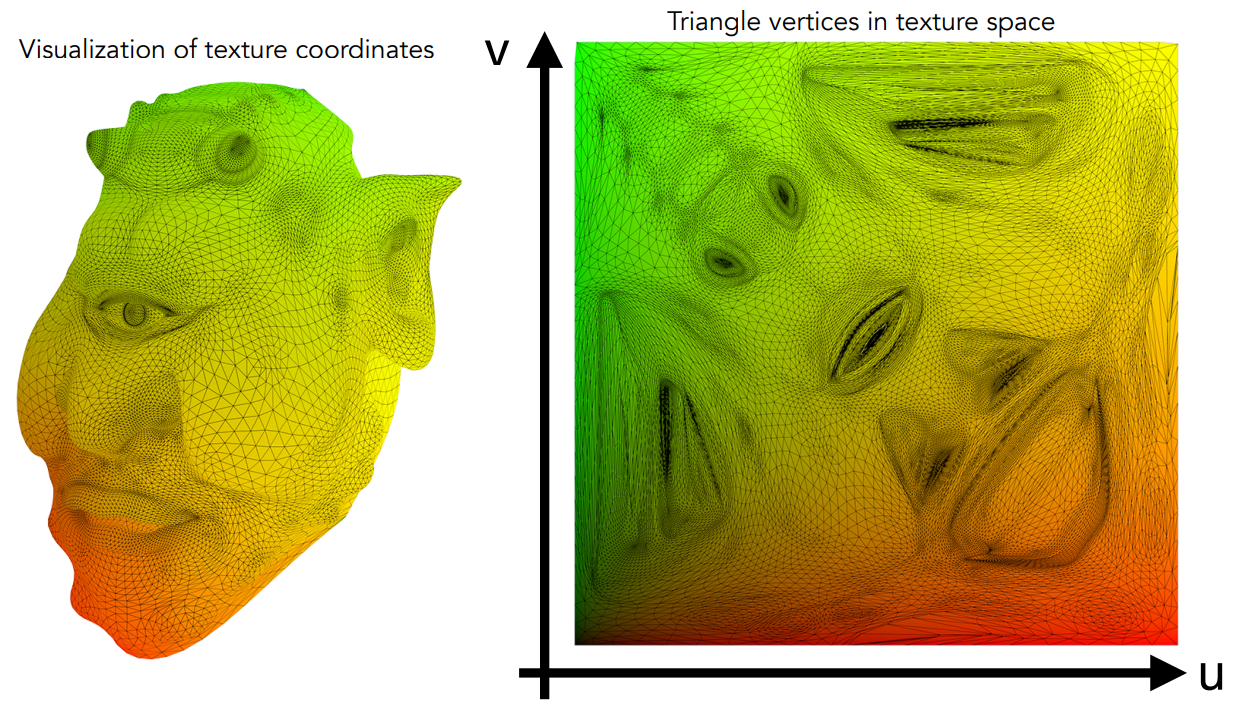
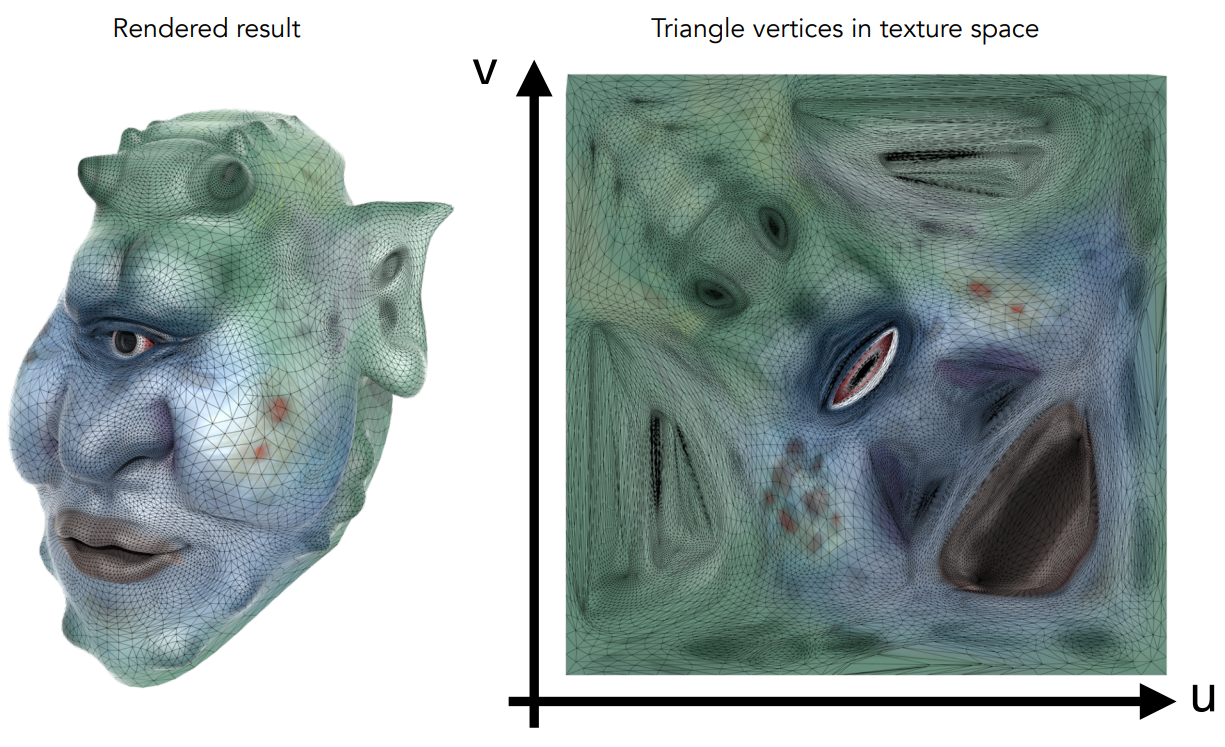
可视化的纹理坐标

纹理是可以复用的，即同一个纹理可以被多次使用。这种纹理在图形学中被统称为无缝纹理贴图（Tileable Texture）。这种纹理的设计需要各种各样的算法，其中一种算法叫做Wang Tiled。

Interpolation Across Triangles:Barycentric Coordinates

三角形的插值：重心坐标

我们为什么要引入插值？

三角形顶点的值都是额定的
平滑过渡

我们使用插值都做了些什么？

纹理坐标插值
颜色插值
法线插值

重心坐标是定义在三角形上的，在三角形ABC构成的平面内，任何一点(x, y)都可以表示成A、B、C这三个顶点坐标的线性组合。

$(x,y)=\alpha A+\beta B+\gamma C \\ \alpha+\beta+\gamma=1$

当系数$\alpha$、$\beta$、$\gamma$都非负时，该点在三角形内；否则在三角形外。如果三个系数之和不为1，那么该点不在三角形构成的平面内。

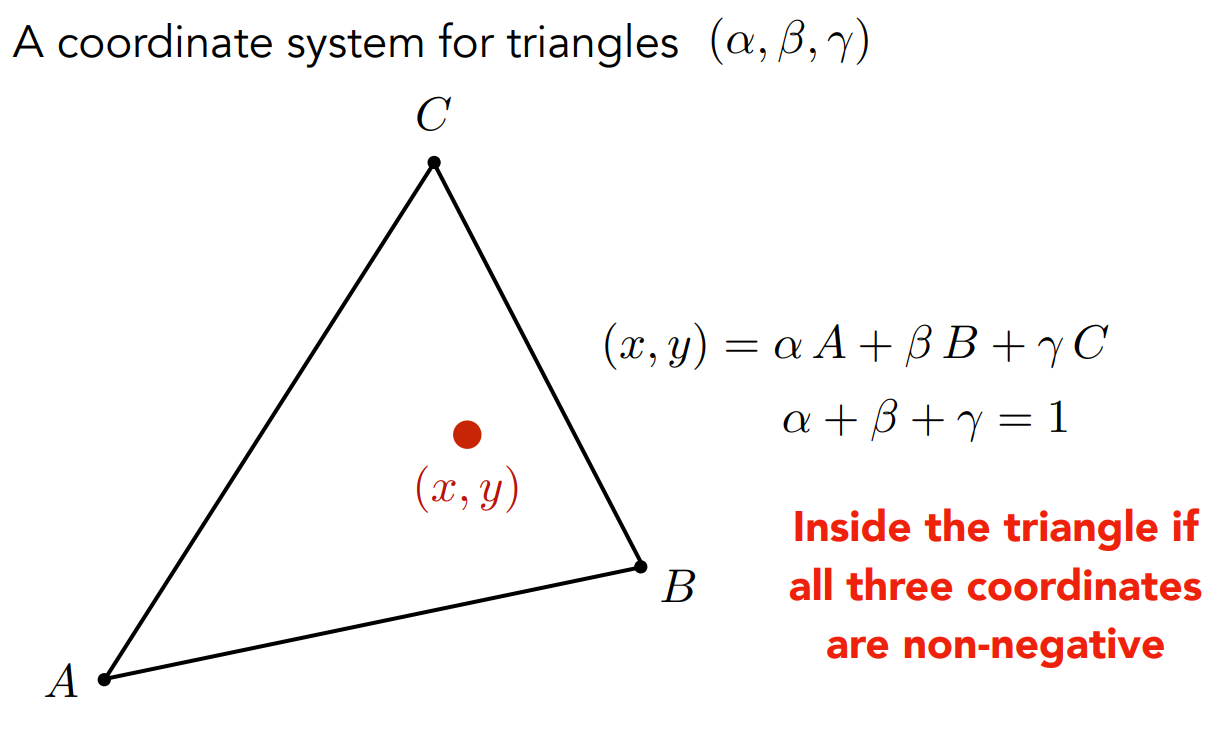
那么三角形A点的重心坐标是多少呢，显而易见：

$\begin{equation} \begin{split} (\alpha, \beta, \gamma) &= (1, 0, 0) \\ (x, y) &= \alpha A+\beta B+\gamma C \\ &= A \end{split} \end{equation}$

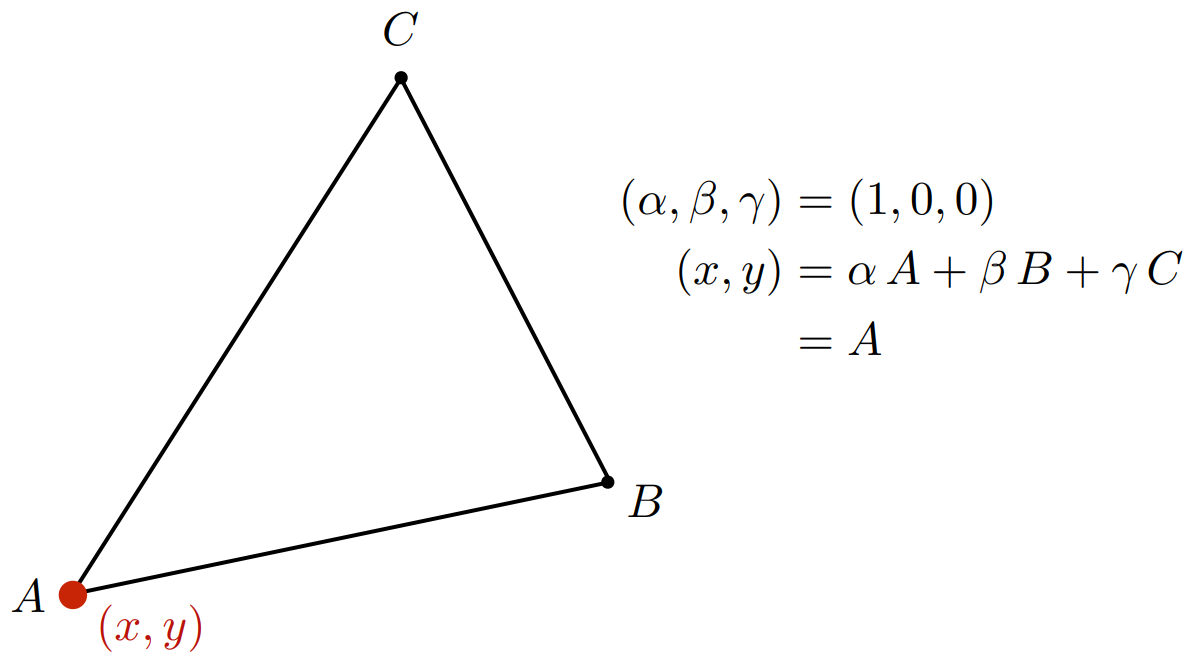
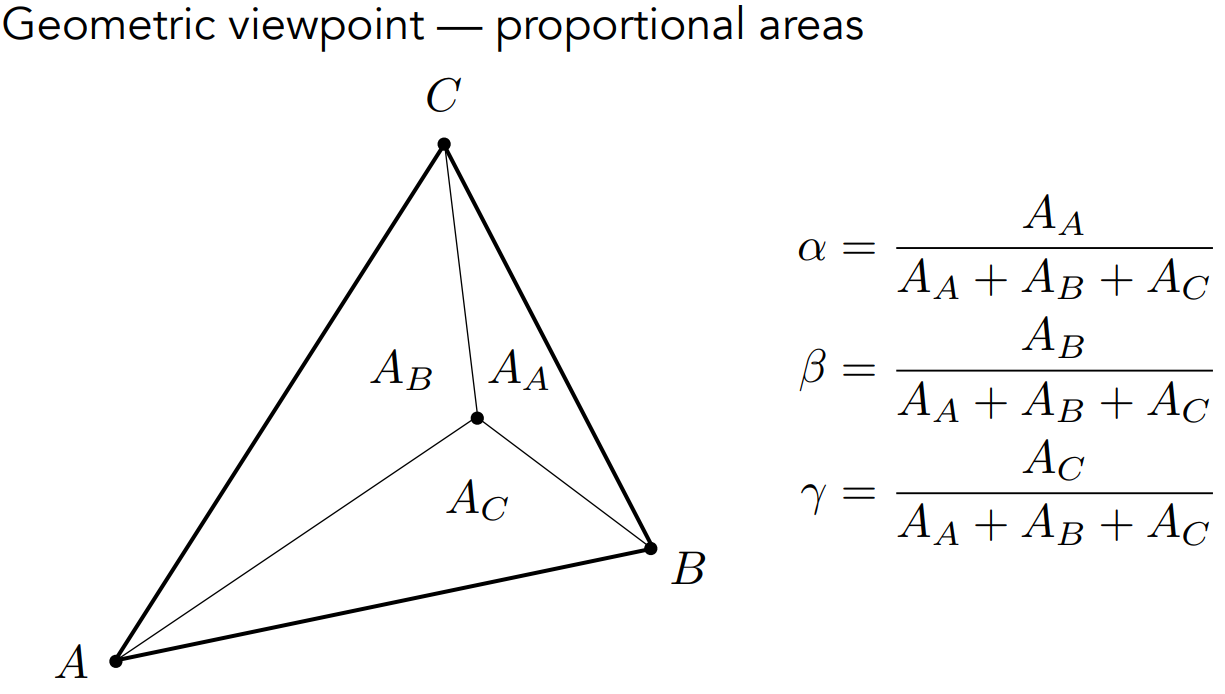
在几何定义下，我们可以通过面积之比来计算三个系数$ \alpha $、$ \beta $、$ \gamma $。

$\begin{equation} \begin{split} \alpha &= \frac{A_{A}}{A_{A}+A_{B}+A_{C}} \\ \beta &= \frac{A_{B}}{A_{A}+A_{B}+A_{C}} \\ \gamma &= \frac{A_{C}}{A_{A}+A_{B}+A_{C}} \\ \end{split} \end{equation}$

在重心坐标系下，三角形的重心是多少呢？

根据重心的性质，重心和三角形的三个顶点连接起来，会将三角形等分为三份，即三个等面积的三角形。那么根据上边的公式可以得出：

$\begin{equation} \begin{split} (\alpha, \beta, \gamma) &= (\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) \\ (x, y) &= \frac{1}{3} A+\frac{1}{3} B+\frac{1}{3} C \\ \end{split} \end{equation}$

同时，三角形的面积可以通过向量的叉乘计算：

$\begin{equation} \begin{split} \alpha &= \frac{-(x-x_{B})(y_{C}-y_{B})+(y-y_{B})(x_{C}-x_{B})}{-(x_{A}-x_{B})(y_{C}-y_{B})+(y_{A}-y_{B})(x_{C}-x_{B})} \\ \beta &= \frac{-(x-x_{C})(y_{A}-y_{C})+(y-y_{C})(x_{A}-x_{C})}{-(x_{B}-x_{C})(y_{A}-y_{C})+(y_{B}-y_{C})(x_{A}-x_{C})} \\ \gamma &= 1-\alpha-\beta \\ \end{split} \end{equation}$

我们需要插值的属性，也同样可以通过重心坐标线性的组合出来。

但是，重心坐标在投影变化下，并不是不变的。所以光栅化中的深度测试，需要先做逆变换，然后对三维空间中的坐标做插值。

Applying Textures

如何进行纹理映射？

先对三角形中的采样点进行纹理坐标插值，得到$(u,v)$坐标，然后在纹理上查询$(u,v)$值，得出这个点上的颜色。我们可以认为这个颜色就是漫反射系数$k_{d}$，然后经过Phong Shading的计算，将这个颜色值设置到物体上，即相当于将图贴到了物体上，且带有漫反射、高光、环境光等效果。

Texture Magnification

纹理的放大，即纹理的分辨率不足

A pixel on a texture — a texel (纹理元素、纹素)

Bilinear Interpolation（双线性插值）

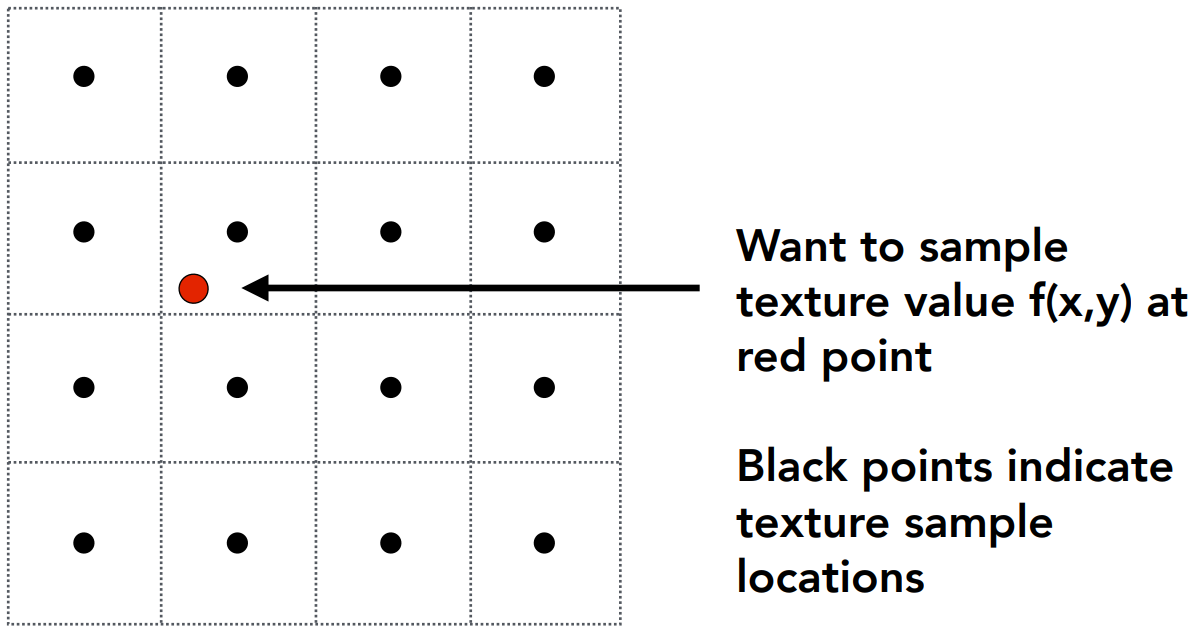
如下图，我们想要在红点处采样纹理值，其中黑点代表纹理采样点。

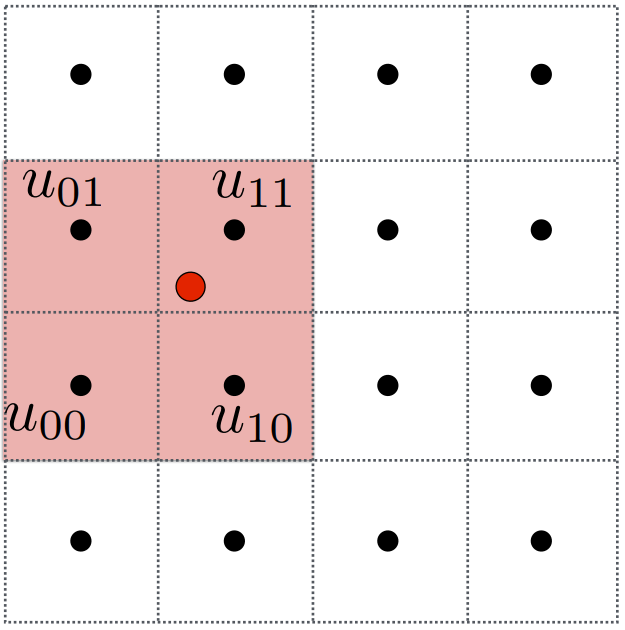
取四个临近的采样点

令两个采样点之间的距离为1，以四个点的左下角为0点，然后可以通过水平距离$s$和垂直距离$t$，找到红点的位置。

通过线性插值（Linear interpolation (1D)）操作，即

$lerp(x,v_{0},v_{1})=v_{0}+x(v_{1}-v_{0})$

当x=0时，插值等于$v_{0}$；当x=1时，插值等于$v_{1}$。

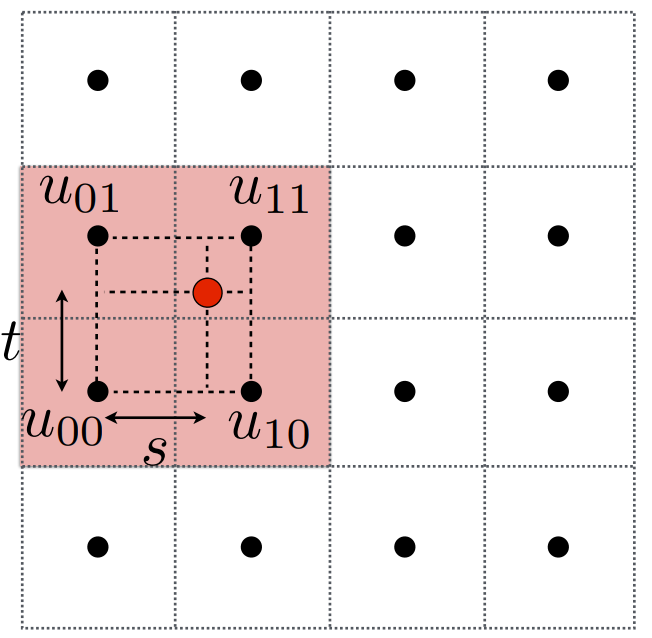
那么，我们对下边这条边，即左下角和右下角这两个点，使用$s$做插值；同理，上边这条边，我们也可以使用$s$对左上角和右上角两点进行插值。即，

$u_{0}=lerp(s,u_{00},y_{10}) \\ u_{1}=lerp(s,u_{01},y_{11})$

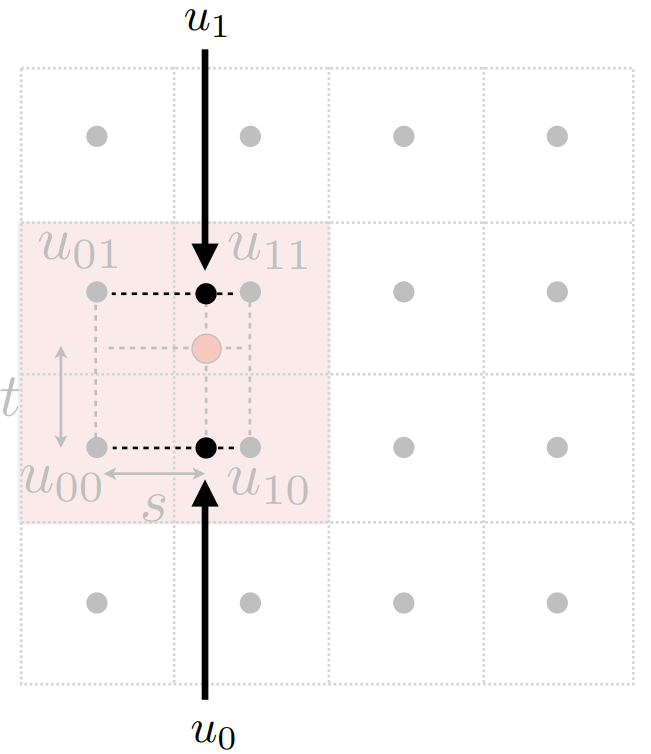
最后，我们再使用$t$做一次竖直方向上的插值。即，

$f(x,y)=lerp(t,u_{0},u_{1})$

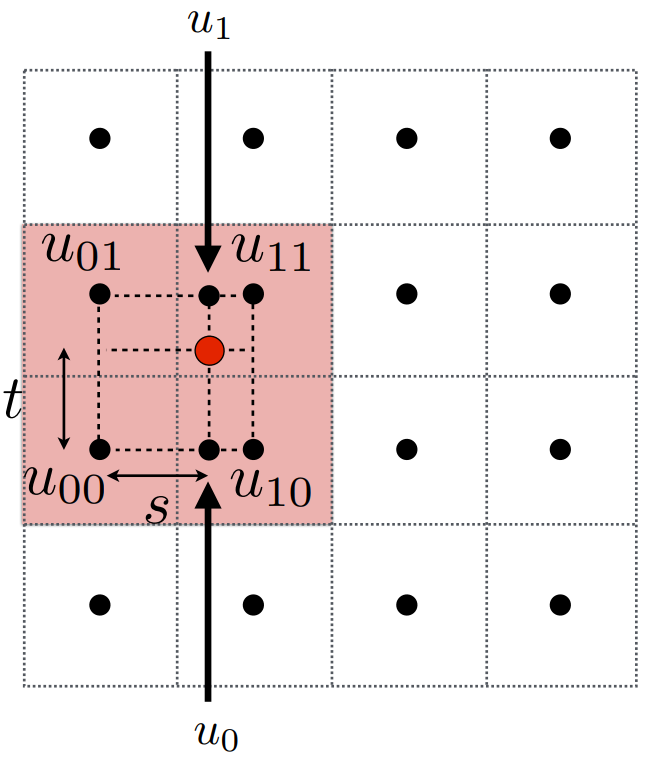
双线性插值通常以合理的成本给出相当不错的结果。

但是，双线性插值（Bilinear Interpolation）也存在一些问题，对于一些更高级的方法，双线性插值的质量还是差一些。

纹理过大，也就是纹理的分辨率过于大

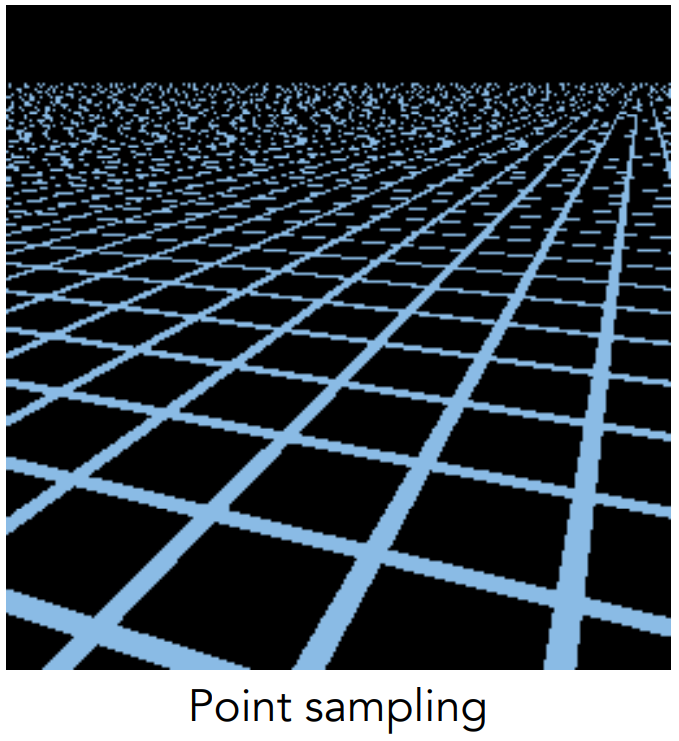
纹理过大，采样后会出现什么问题呢？

没错，近处会出现锯齿，远处会出现摩尔纹。

为什么会出现这种走样的情况？

因为近处一个像素所覆盖的纹理上的区域相对较小，但是在远处一个像素就覆盖了一片纹理区域。

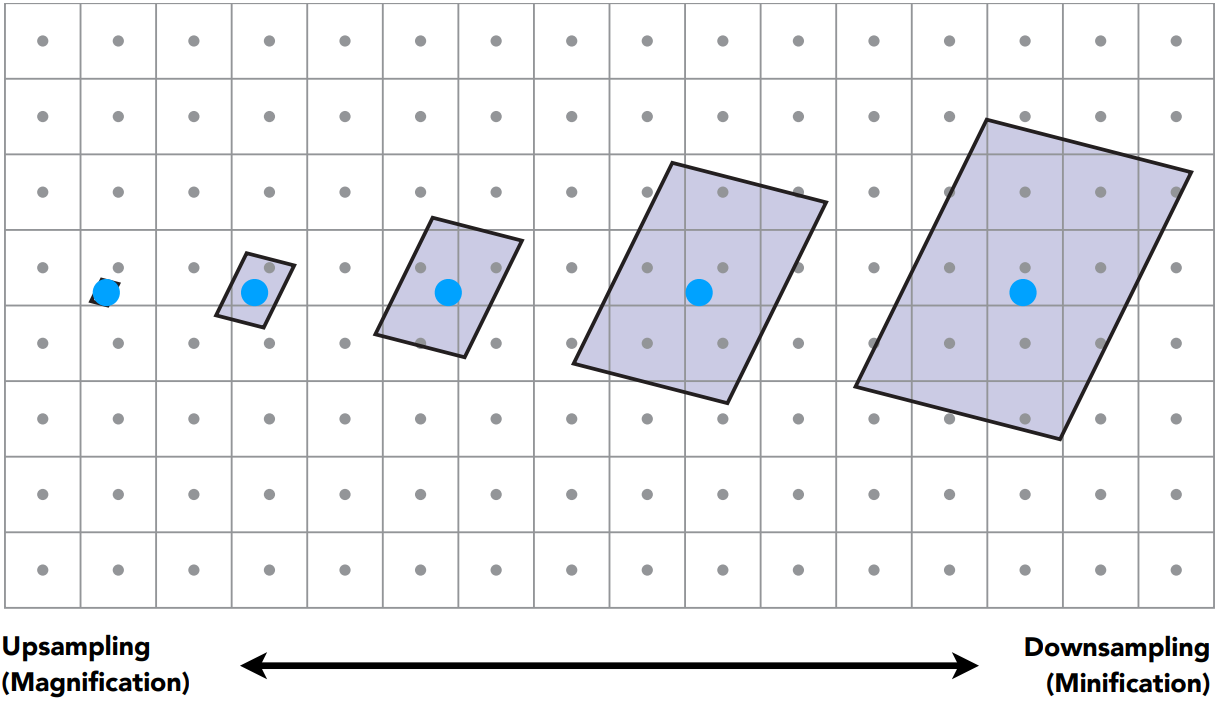
那么我们依旧可以采用超采样的方法，得出一个不错的结果，但是使用超采样会有一个问题，那就是开销问题。增加采样点，必然会使整个算法变得特别慢。当然，我们也不希望一个算法会变得超级慢。

如果不使用超采样方法的话，我们仅需要得到该像素所对应的范围内的平均值即可。范围查询不只是我们用的这一种应用——平均查询，还有很多类型的范围查询，比如说查询范围内的最大值、最小值等。

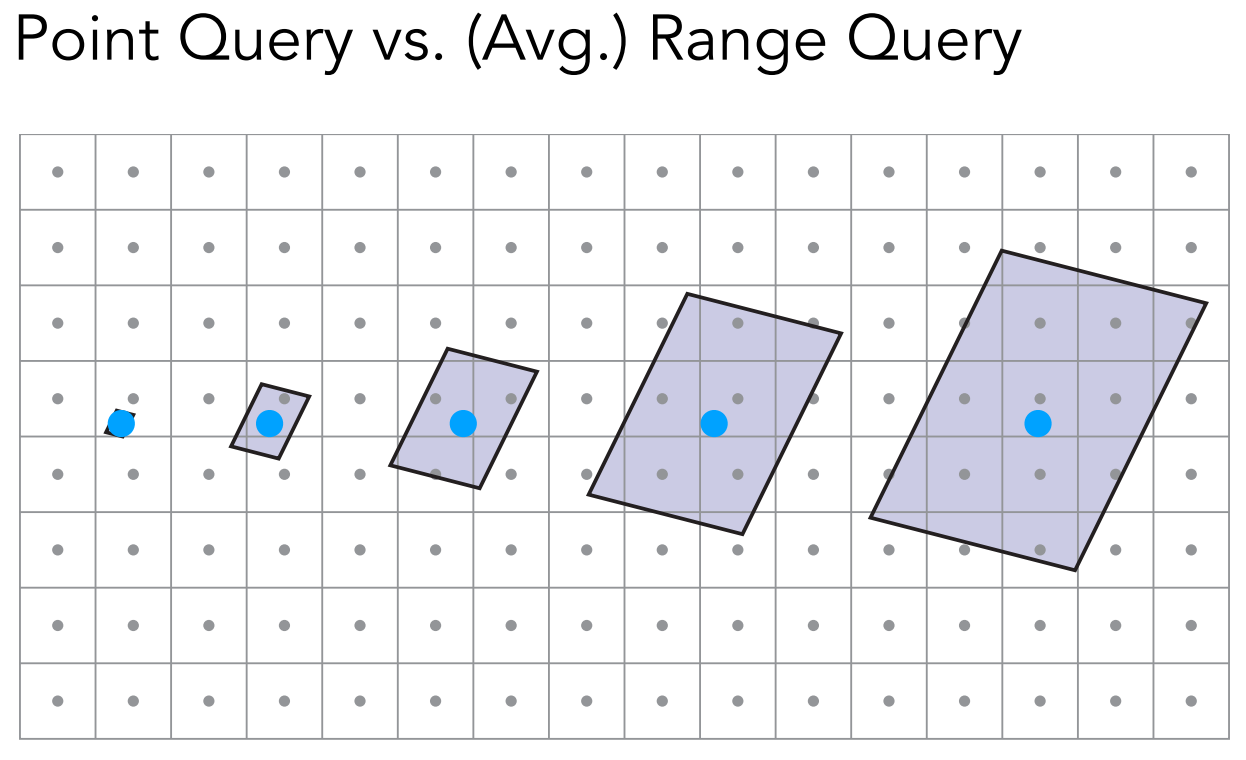
不同像素在纹理上的覆盖对应不同大小。

Mipmap

允许（快速，近似，正方形）范围查询

“ Mip”来自拉丁语“multum in parvo”，意思是有很多不同的小的东西。

其实Mipmap就是从一张图生成一系列图，假如说第一张图叫做Level 0，那么我们可以生成更多更高层的纹理，使得每一层$i$，都是第$i-1$层的长和宽缩小一半，直到最后剩下一个点。一共$log_{2}n$层，$n$为分辨率。

对应到Mipmap中，我们生成的是如下图这样的东西，第0层为原始的图像，上边总比下边小一半。

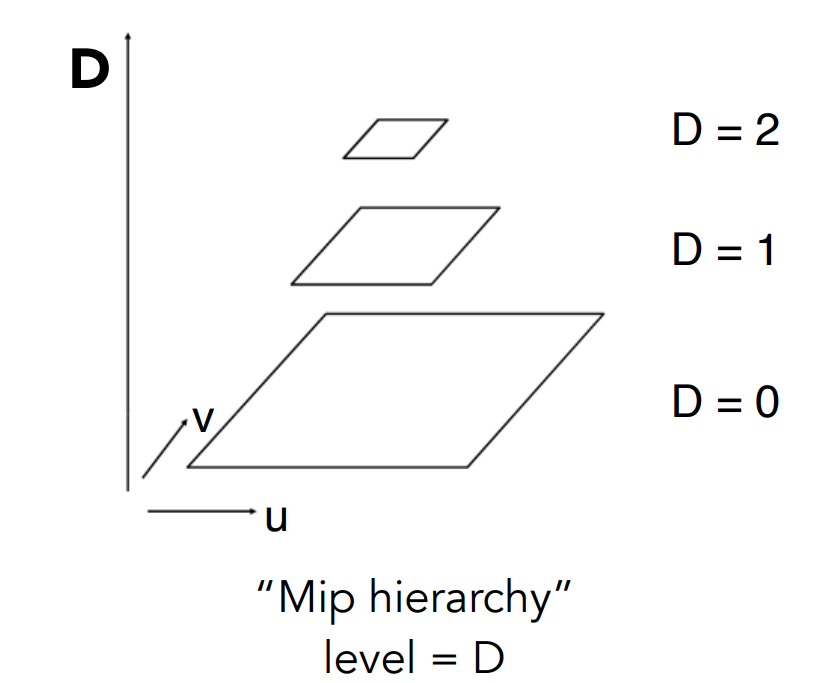
所以在计算机视觉界，大家不把它称作Mipmap，而是称作Image pyramid（图像金字塔）。

Mipmap所造成的额外存储仅是原来的$\frac{1}{3}$，使用级数求和可以计算得出。

$\sum_{n=1}^{\infty}{1+\frac{1}{4^n}}$

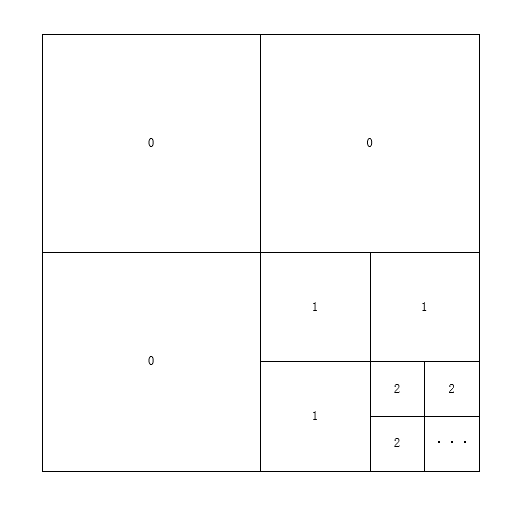
还有一种理解方式，可以把每一层的存储都乘以3（不影响最终结果），并把第0层的三份分别放在左下角、左上角、右上角，然后把第一层的三份分别放在空置的右下角方块中，并且依旧按照左下角、左上角、右上角，那么右下角再次空出，以此类推把剩余层填入剩余的空间。则会发现，最外层除了三份0层，剩下的层都放在了右下角，所以得出$\frac{1}{3}$。

计算Mipmap层

任何像素都会有一个对应的映射在纹理上的区域

如下图，要计算左下方的红点所占据的像素的覆盖面积，我们可以取这个像素的中心点和它相邻像素的中心点，分别投影到纹理上去。

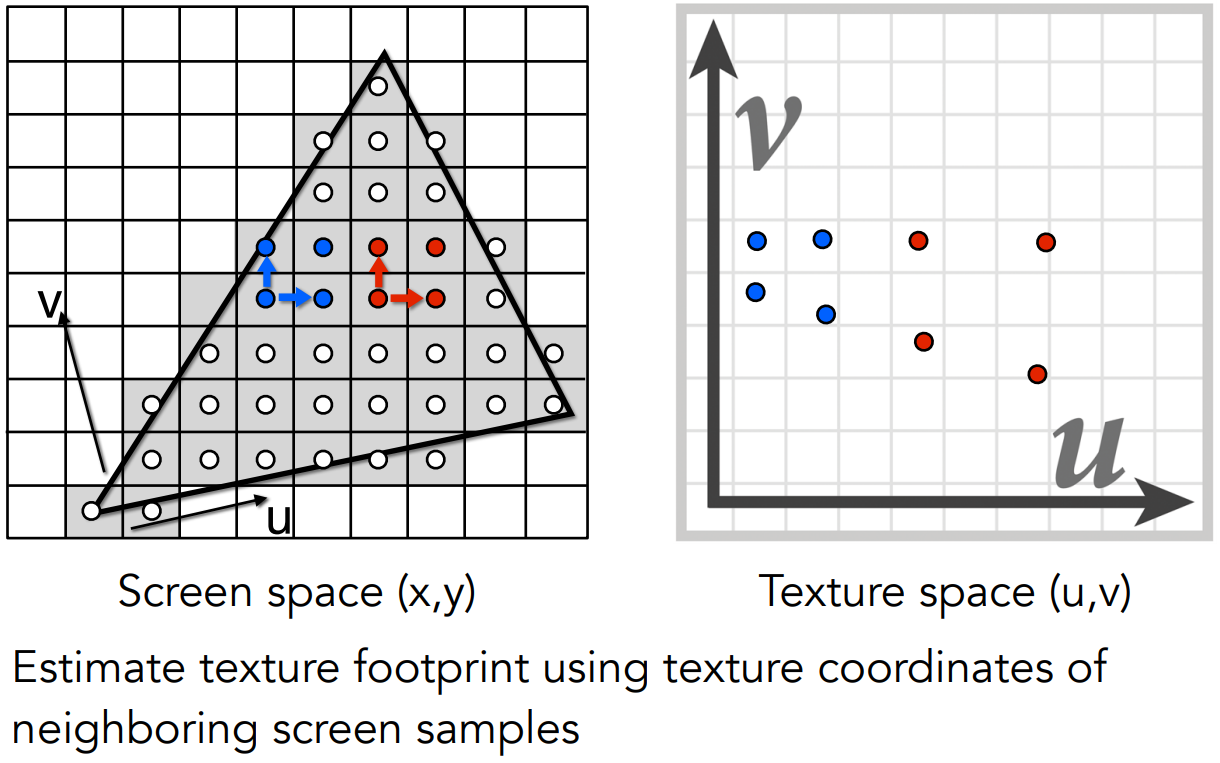
求出纹理上，该点相对于上方相邻点和右方相邻点的长度，就可以近似计算出这个像素在纹理上所占区域的边长。这个边长就作为以该像素中心点为重心，所占正方形区域的边长。

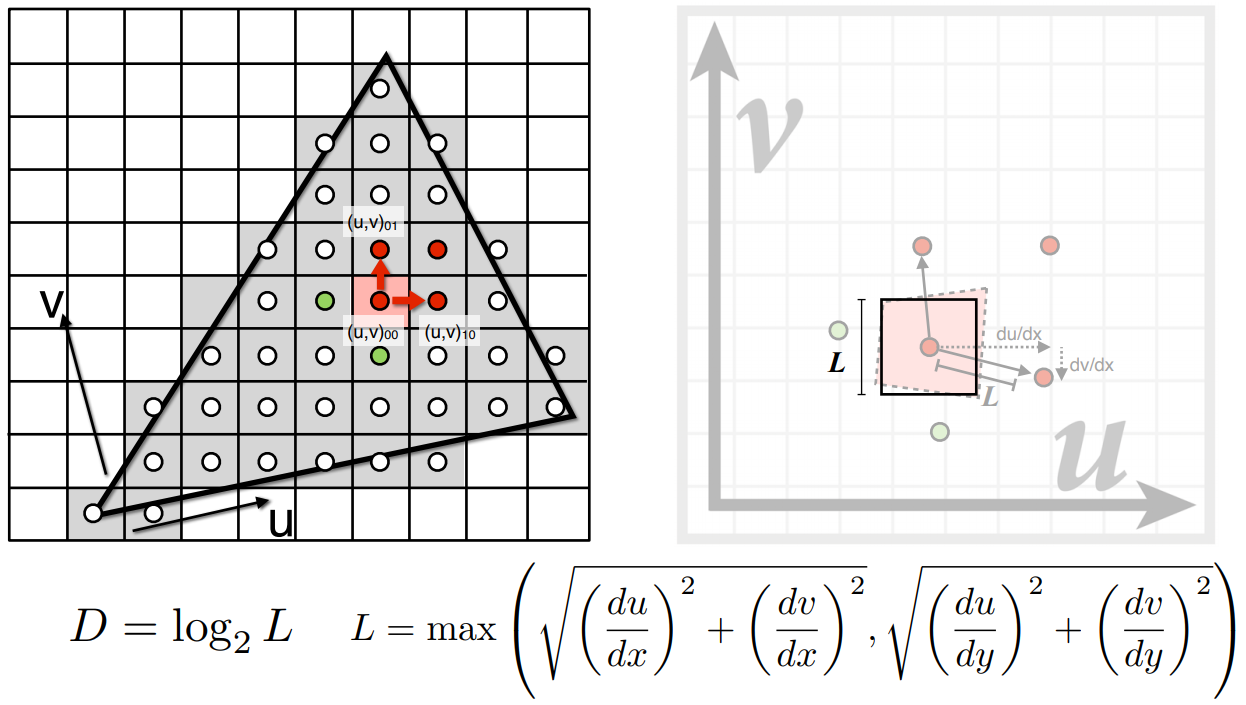
接下来，我们应该如何根据预计算好的Mipmap，去查询这个边长为$L$的正方形区域内的平均值？

我们可以假设，如果这个正方形的区域大小是1x1，就是一个像素，那我们可以在没有做过Mipmap的最原始的纹理上找对应的像素。

如果这个正方形的大小是4x4，那我们可以得出这个区域一定会在第2层上变成1个像素。为什么呢？我们可以思考一下，这个区域的大小是4x4，是指在最原始的图片上的大小是4x4。那么经过第一层Mipmap后，这个区域会变成2x2，然后经过第二层Mipmap之后，这个区域会变成1x1。

这个$L*L$大小的区域，一定会在$log_{2}L$层上对应到1个像素。也就是说我们只要计算出这个区域在第几层变成了一个像素，那么我们就可以去查找那个像素，即立刻得出这个区域的平均值是多少。

如果说对于每个像素，我们都计算它投影到纹理上对应的区域，然后根据这个区域的大小，计算出应该在第几层Mipmap上去找这个像素的平均值，那我们就可以做一个可视化。

虽然在上图中，我们发现这些颜色有些渐变，但是会发现一个问题，那就是这些颜色的变化并不连续。因为我们只查询了第0层、第1层、第2层等等的整数层，如果我们想要查询第1.5层、第1.8层，应该怎么办呢？

那当然是使用插值

假设我们想查询第1.8层，那么应该先查询第一层，再查询第二层。在这两层内部，分别使用双线性插值，把所在的这两层上的查询先做出来；然后把这两层插值得出的值，再做一次插值，即相当于在层与层之间做了一次插值。一共做了三次插值，我们把它称作三线性插值（Trilinear Interpolation）。

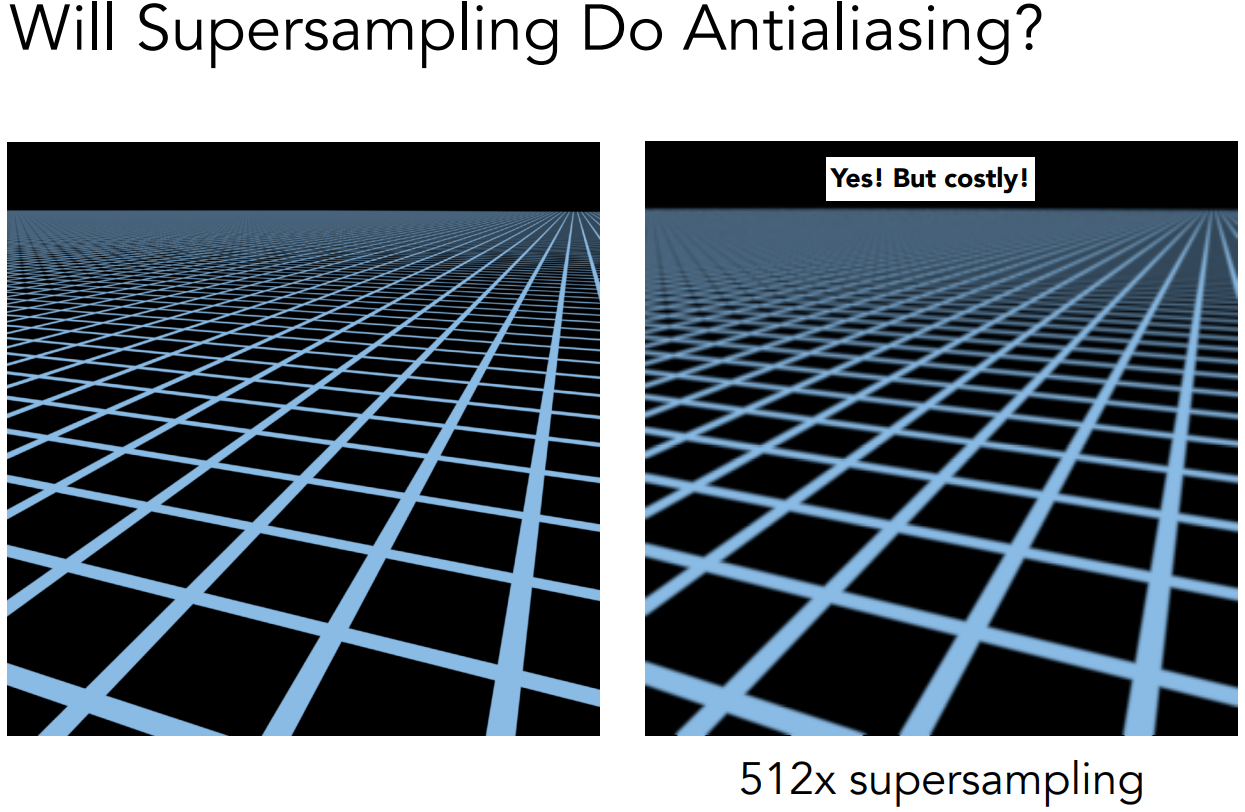
再来对比一下原图、超采样、Mipmap。

原图：

使用512x超采样：

Mipmap：

我们会发现Mipmap似乎并不太对，远处全部模糊了起来。

原因在于，Mipmap只能查询到正方形区域内的插值。我们可以使用各向异性过滤（Anisotropic Filtering ）。

Mipmap所做的事情就是在原图上一直把长宽缩小一般，那么对应到下图中其实Mipmap就是做了对角线上的计算。但是有一些图需要作不同长宽比的预计算，这个就是Mipmap中所没有的。

各向异性过滤

各向异性是指，在不同的方向上表现各不相同。我们原本认为在正方形的水平和垂直方向上，表现完全相同，就叫做各向同性。

我们可以看到上图中，每一行都做了水平方向上的压缩，每一列都是垂直方向上的压缩。它相比于Mipmap多了一些水平方向和垂直方向上不均匀的压缩。

通过这样的一种方式的预计算，就可以查询到任何一个被压扁了的图的位置，即可以查询原图的一个矩形区域，而不用被限制在一个正方形的区域内。

因为屏幕上的任何一个像素映射在纹理上，不一定都是一个规律的形状，很可能出现斜着的、极细的形状，如下图。

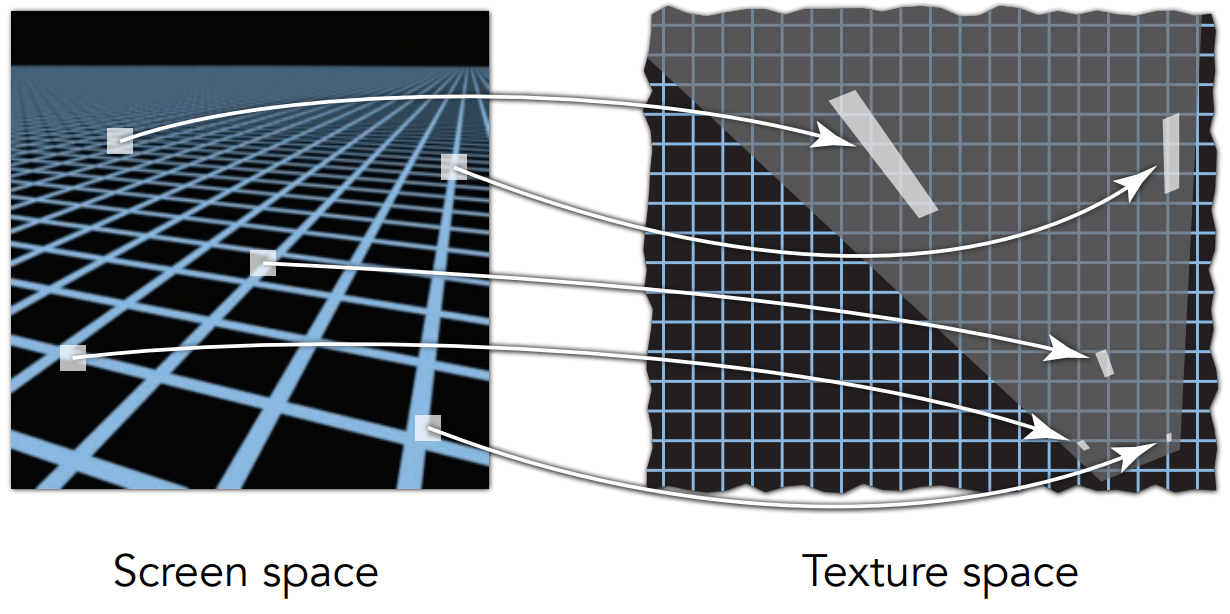
例如上（右）图中，左上方斜长条区域，如果我们把它近似成一个正方形区域，就相当于求了一个更大区域的平均，所以会造成Overblur（过于模糊）。

如果我们引入各向异性过滤，例如上（右）图中，右上方的长条区域就可以得到一个近乎完美的解决，因为各向异性过滤允许我们对这种长条形的区域做一个快速的查询。

我们可以通过上边带有卫星的那张图片分析出，各向异性过滤所生成的图，总共的开销是原本的3倍（原图占左上角的1/4）。各向异性过滤生成的图有一个名字，叫做Ripmap。而Mipmap所需的开销比原本多1/3，这里可以供我们参考一下。

如果大家经常打游戏的话，会接触到一个各向异性过滤相关的概念，就是多少x，这里的x其实指的就是计算多少层，比如说2x指的就是方向上压缩了一次，就是上边带有卫星的那张图片中的左上角四个卫星的区域，以此类推，4x就是在2x的基础上又压缩了一次，就是上边带有卫星的那张图片中的左上角九个卫星的区域，即左上角$((log_{2}{n})+1)^2$个卫星，n代表nx。

我们会发现，n的增加，最后的结果会逐渐收敛至原图的三倍，也就是说各向异性过滤的存储量和用户开nx的关系不大。应用各向异性过滤，只要显存足够，其实和计算力基本没有关系，所以在游戏中将各向异性过滤开至最高也几乎不会对游戏有性能的影响。

但是各向异性过滤仍然不能解决斜着的区域，要解决这个问题，可以使用一些另外的方法，比如EWA filtering。

EWA filtering

Use multiple lookups
Weighted average
Mipmap hierarchy still helps
Can handle irregular footprints

任意一个不规则的形状都可以被拆分成很多圆形，以覆盖这个不规则形状。例如，有一个椭圆形（如下图），可以把它拆分成三个不同的圆形，然后每次去查询一个圆形，然后多次查询，自然就可以去覆盖一个不规则的形状。但是代价就是牺牲时间，因为查询时需要耗时的。

查看评论

1. Illumination & Shading